Secrets de la science et de la géométrie
Le système visuel - binoculaire (stéréoscopique) système optique de nature biologique, évolutionnaire surgi chez les animaux et est capable de percevoir le rayonnement électromagnétique dans le spectre visible (lumière), créant un sentiment de la position des objets dans l' espace. Le système visuel assure la fonction de vision.
La vision de la (perception visuelle) humaine - le processus de traitement des images psychophysiologiques d'objets du monde, menées par le système visuel, et vous permet d'obtenir une idée de la taille, la forme ( à long terme) et la couleur des objets, leur position relative et la distance entre eux. Selon diverses sources, de 80% à plus de 90% des personnes d'information reçoivent par la vision.
Géométrie (de l'ancienne terre grecque et mesure.) - Une branche des mathématiques qui étudie les tendances et les relations spatiales, ainsi que leurs généralisations.
Nous avons utilisé pour faire confiance à vos yeux et de ne jamais poser la question, pourquoi le même objet apparaît plus grand près et de loin finement? Ou pourquoi différentes tailles éléments apparaissent parfois la même taille? Mécanismes de très complexe, mais certaines de ses caractéristiques peuvent déjà être expliqués sur la base des représentations géométriques.
Quel est l'angle de vue
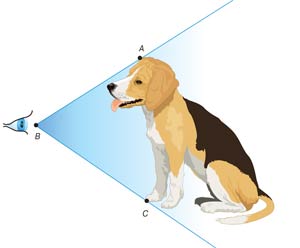
La taille angulaire de l'objet - ce qui est l'angle de vue à partir duquel l'objet entier est visible (dans ce cas - angle ABC).
Chaque objet a une dimension linéaire: longueur, largeur et hauteur. Mais dès qu'il pénètre dans notre champ de vision, il prend une autre dimension - le coin. Voyons voir ce que cela signifie. Quand on regarde le sujet, puis par chaque point peut être effectuée à partir du faisceau des yeux, appelée la ligne de mire. Il est clair qu'il y aura un nombre infini. Les deux faisceaux forment un angle de vue. Ce point de vue à partir de laquelle le sujet est considéré comme un tout, et a appelé la taille angulaire de l'objet. Comme tout autre angle plan, elle est mesurée en degrés, minutes, secondes, ou en radians.
Le concept de taille angulaire est utilisé en optique géométrique, la géodésie, l'astronomie. Il se trouve dans la géométrie, mais ici, ils disent à propos de l'angle de vue à partir de laquelle les points mentionnés "vu" ce segment - la hauteur de la figure, son diamètre et ainsi de suite.
La taille angulaire dépend du choix du point d'observation, ce qui est facile à voir, mesurer à partir de deux points situés à des distances différentes de l'objet. Selon la nature de l'objet de l'angle sous lequel il est visible, déterminée au moyen de dispositifs spéciaux, par exemple, pour les mesures sur le site à l'aide d'un théodolite, pour déterminer la hauteur des objets célestes dans le ciel - un sextant, etc.

Mesure de la hauteur de la lumière au moyen du personnel de Jacob.
Dans les temps anciens, avec le même objectif utilisé un des outils les plus primitifs. L'un d'eux - le personnel de Jacob, le prédécesseur du sextant moderne. Ce fut une tige coulissante sur laquelle le rail transversal; sur la tige avait souffert division, correspondant à quelques coins (leur protractor pré-mesurée). L'observateur offrant une extrémité du personnel à l'œil, l'autre dirigée vers le côté de l'objet mesuré, puis déplacé vers le rail aussi longtemps que ce n'est pas à une extrémité "touche" la ligne d'horizon, et l'autre - un objet céleste. Après cela pourrait seulement «prendre des lectures" - pour voir ce que la division de la tige correspond au râteau. Cet outil pratique et simple est facile à faire vous-même, il est tout à fait approprié pour une mesure exemplaire d'angles dans un plan quelconque.
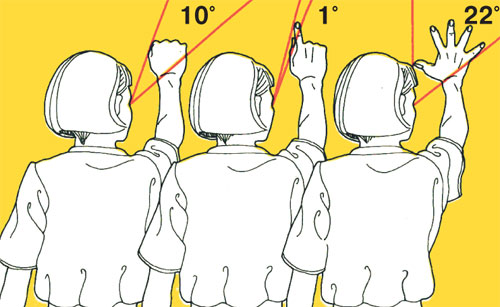
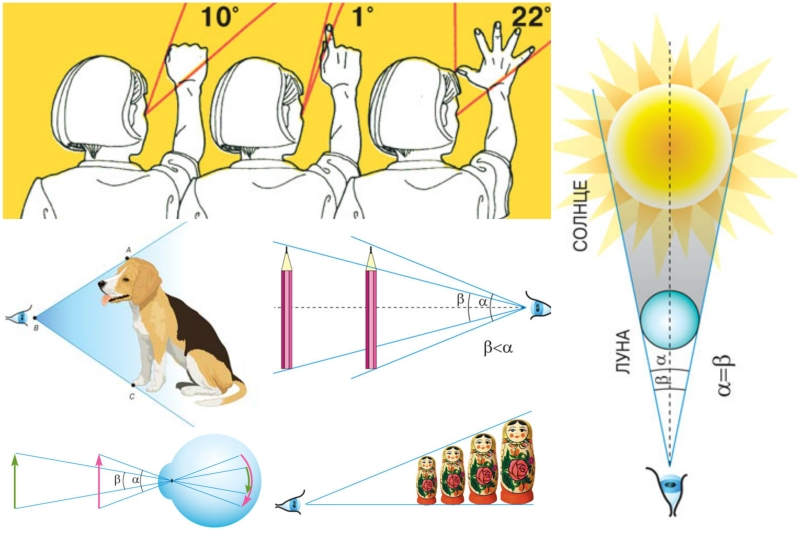
Hand - protractor naturel.
Enfin, pour évaluer la taille angulaire de l'objet peut être littéralement «mains nues». Protractor remettra si, bien sûr, de connaître quelques-uns des coins. Par exemple, l'ongle de l'index tendu en face de la main, nous pouvons voir à un angle d'environ 1 °, poing -. À un angle de 10 degrés, et l'écart entre les extrémités du pouce espacées et le petit doigt -. À un angle de 22 degrés.
La taille et la distance angulaire
La taille angulaire de l'objet - est pas une constante et dépend de la distance entre les yeux du sujet: le sujet plus loin, plus l'angle de vue à partir duquel il est visible.
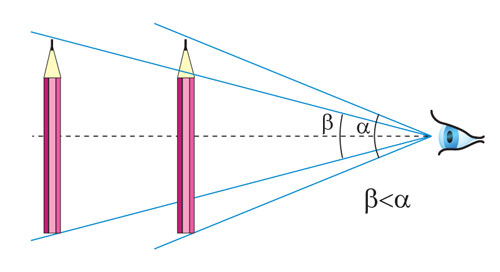
La même chose peut être visuellement différentes tailles en fonction de la distance de l'œil de l'observateur.
Pour comprendre la raison de ce phénomène, rappelons-nous que sur la rétine de l'image du sujet est inversé et réduit. Lorsqu'un objet est supprimé, son image sur la rétine devient moins, et donc il semble diminuer. Lorsque cette distance est réduite contraste de l'image, l'augmentation et le sujet semble augmenter. Sur le plan géométrique, cela signifie que l'angle de vue est inversement proportionnelle à la distance à l'objet.
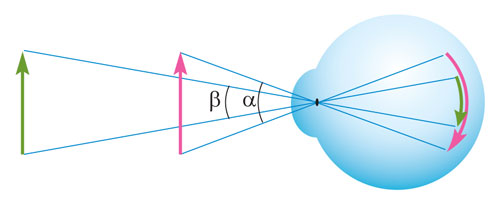
L'image de l' objet sur la rétine de l'oeil est obtenue inversée à l' envers (arrière) et réduit.
Cette fonctionnalité aide à comprendre certaines de nos actions et les phénomènes qui nous entourent. Pourquoi, par exemple, pour afficher les détails sur les peintures murales ou les petits caractères sur la page du livre, il est nécessaire d'aborder la toile plus proche ou apporter texte aux yeux. La réponse est simple: nous avons besoin pour agrandir l'image sur la rétine, et devrait augmenter l'angle de vue de cela, ce que nous faisons, en réduisant la distance du sujet.
Un autre exemple. Imaginez deux lignes parallèles distantes "emballement" (rails, le bord d'une route droite). Ils semblent «converger» à un moment donné. La même impression est créée par des rangées de poteaux télégraphiques et des arbres le long de la route. Vision si vous essayez de nous convaincre que, contrairement aux lois de la géométrie, les lignes parallèles se croisent. Mais ceci est seulement une illusion qui se produit en raison d'une réduction visible de la distance entre les lignes qui se déplacent à une distance.
Sous un angle
Souvent, face à une situation différente. Si nous considérons les objets de la même forme, mais différentes dimensions linéaires dans le même angle de vue, il semble que leurs tailles sont égales. Ceci est confirmé par une expérience simple. Aligner sur la croissance de certaines poupées, et en les regardant de la très petite figure, puis se déplacer lentement, sans changer la direction d'observation. Vous verrez les poupées commencent à «fusionner», bloquant un autre. Enfin, lorsque vous vous éloignez une certaine distance, verra une seule poupée imbriquée - le plus proche de vous. Si nous passons maintenant les chiffres sur les côtés de sorte qu'ils étaient parfaitement visibles, les poupées visuelles apparaîtront de la même taille.
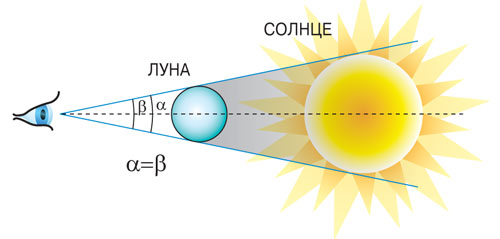
La géométrie d'une éclipse solaire totale.
Un phénomène similaire peut être observée dans la nature. Par exemple, l'éclipse solaire disque lunaire complet obscurcit exactement le soleil. À ce stade, un observateur sur la Terre voit les deux corps célestes dans le même angle de vue. Pour voir un tel événement unique ne serait pas possible si les dimensions linéaires du Soleil et la Lune, ainsi que la distance de leur part à la Terre ne consiste pas dans une certaine relation mathématique.

Sous un angle dimensions linéaires visibles des objets se ressemblent.
En termes de géométrie dans les deux cas, nous avons affaire à la similitude des chiffres, ou plus précisément, une homothétie avec le centre coïncidant avec l'œil de l'observateur. Par conséquent, si les deux sont similaires dans la forme de l'objet peut être vu sous le même angle de vue, leurs dimensions linéaires sont différents en autant de temps, combien de fois les différentes distances aux objets. Ainsi, les diamètres du soleil et la lune (D et d) et la distance entre les corps à la terre (L l) sont connectés par la simple formule:
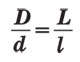
Nous avons divulgué aucun moyen tous les secrets. Caractéristiques voir, quand on regarde avec les deux yeux, une explication de certains de l'illusion visuelle, la création d'effets visuels dans l'architecture et la peinture.
Candidat des sciences pédagogiques Marina Egupova et Natalia Karpushina via nkj.ru


Commentaires
Commentant, gardez à l' esprit que le contenu et le ton de vos messages peuvent blesser les sentiments des gens réels, montrer du respect et de la tolérance à ses interlocuteurs, même si vous ne partagez pas leur avis, votre comportement en termes de liberté d'expression et de l' anonymat offert par Internet, est en train de changer non seulement virtuel, mais dans le monde réel. Tous les commentaires sont cachés à l'index, le contrôle anti - spam.