| section Accueil
Production, Amateur Radio amateur avions de modèle, fusée Utile, divertissant |
maître furtif
électronique physique de la technologie invention |
espace Mystery
Mystères de la Terre Secrets de l'océan infiltration section Carte |
|
| Utilisation de matériel est autorisé à titre de référence (pour les sites - hyperliens) | |||
Navigation: => |
Accueil / Invention / De nouveaux types de moteurs / |
|
WONDER ROUE OU "Perpetuum Mobile"?
- La géométrie -
Voir aussi: |
Le cercle dans la géométrie est une figure simple avec des formules bien connues pour trouver l'aire et de la circonférence d'un cercle. Le libellé ressemble à la figure, dont la distance du centre à un point quelconque de la circonférence sont égales. Cette distance est indiquée par un rayon "R" et est le point de départ pour la construction d'un cercle. Après avoir déterminé le nombre de "Pi", ce chiffre est devenu plus clair et plus clair. La perfection mathématique correcte du cercle attire, mais limite aussi son utilisation.
Offrez chaque figure appellera autour et essayer de prouver qu'il est un cercle. Pour établir une relation de famille, d'abord changer la perception même du cercle en retirant son rayon composant. Et surtout le libellé de ce chiffre Radius diamétralement. Cercle a appelé la figure, dans laquelle toutes les lignes se croisent au centre de son égale. Pour changer et trouver un rayon de la zone de formule diamétralement. égale à la surface d'un cercle (temps de circonférence du diamètre) et diviser par quatre. Le mot périmètre est pas un hasard, parce que cette formule donne la zone et l'autre
figure-carré. Le périmètre de la circonférence et la somme de tous les côtés du carré. Pour le diamètre de la prise et la longueur de la place. La zone du cercle et le carré peut être lié et de l'intérêt. aire d'un cercle est de 78,5% de la superficie d'un carré qui tient dans le cercle. Mais la base pour de nouvelles constructions, cette formulation évite toujours le rayon.
Pour créer un nouveau cercle aura besoin d'une géométrie de l'outil simple, représenté sur la figure.

outils géométriques
Il est un bar transparent en verre organique, sous la forme d'une ligne haute. Au milieu d'un trou longitudinal au moyen de deux crayons coulissantes, qui sont faciles à verrouiller les points requis. Entre eux, et coulissant librement, permettant à la broche au dispositif d'appuyer sur l'instrument à la feuille de dessin. En plus d'utiliser un outil comme une règle, il peut être utilisé comme un compas. Utilisation de la broche et un crayon (ou deux, mais à égale distance de celui-ci) obtenir une boussole. Mais sa principale application à utiliser comme un «miroir», est la suivante.
Prenez l'une des formes simples - carré et trouver l'intersection des diagonales régler la broche centrale sur elle et nous fixons des crayons dans les coins en diagonale. Puis, en tenant la broche, tenir un crayon autour du périmètre de la place et le faire afficher un autre crayon.
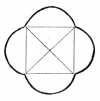
Voir la photo d'exemple la construction
De même, en utilisant cet outil, qui est, en prenant la ligne droite maximale se croisant au centre de la figure, nous obtenons des résultats intéressants.
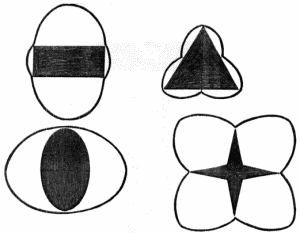
Des chiffres similaires, contrairement à leurs «parents» mathématiques, apprécié la nature, la création de différents types de la flore et de la faune.
Basé sur le retour, la prise de certains types d'organismes, ou des plantes peut être réapprovisionné arsenal de formes géométriques. Mais où sont les mécaniciens et le cercle? Le cercle est le seul chiffre ne donnant pas l'affichage, ou plus précisément, ils sont entièrement déclarés - un cercle avec son reflet. représenté par la figure du même est aligné avec son écran, car il est également en train de tourner. Pour éliminer toute confusion à l'avenir, nous serons appelés le cercle normal - rayon (ou mort) autour. Mathématiquement, pour un seul diffèrent de cette gamme, présente le chiffre devrait être appelé sans cercle de rayon.
Pour simplifier la démonstration de sa création, nous prenons comme un cercle de base Radius.
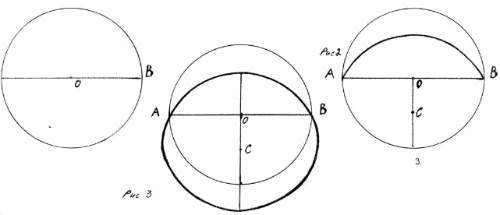
Tracez une ligne horizontale "AB" traversant le centre "O" Fig.1. De ce point, nous laissons tomber la perpendiculaire et choisissons tout point "C" sur elle. En installant cette (appeler l'affichage du point) boussoles point rejoindre les points A et B, la figure 2. Maintenant, en utilisant nos outils - un miroir, obtenir une carte de la courbe "AB" à travers le centre de la "O" la fermer (Figure 3.). Donc, nous avons obtenu le cercle figuru- désiré avec un diamètre égal au cercle à partir de laquelle a commencé le travail.
Un chiffre similaire peut obtenir un affichage en trois dimensions de rayon-cercle sur
plan à deux dimensions, bienvenue artistes tous bien connus.

Le point «C» peut être sélectionné, et à l'intersection de la perpendiculaire à la circonférence, et il est possible pour un cercle. La distance maximale entre le point central "C" est le diamètre de la distance.
Depuis le centre du cercle de rayon-déposer la perpendiculaire du cercle, prendre une distance de boussole "AB" et hors de voitures A ou B et la note sur le point perpendiculaire "C". Radius obtenir les meilleures conditions possibles (figure 1). Avec l'augmentation de la distance le cercle se déplace dans une autre figure (Figure 2).
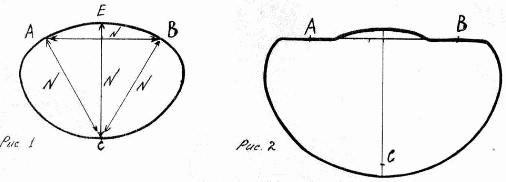
A affichage maximum plage de point "C" apparaît sur la circonférence du cercle de rayon libre-que nous avons pris le diamètre circulaire du cercle pour la distance de construire sans rayon de cercle (Figure 1). Connexion des points A et B du point de boussole "C" apparaît dans le point "E" avec la distance d'un point "C" égale à la distance AB et BC. Mais le rayon ne peut pas être égal au diamètre. En outre, une ligne AB (Figure 1) et divise le rayon de cercle sans milieu, mais pas sur la zone et le nombre de points constituant un cercle.
Paradoxalement, depuis la seconde moitié de la circonférence de la VA a une longueur bien supérieure à l'AB. Être une figure fermée, ont à faire valoir ce point à demi BA longueur supérieure à la moitié opposée d'entre eux sur l'AB.
Pour argumenter sur l'égalité de la surface d'un carré, avec un côté égal au diamètre d'un cercle avec une superficie de pas de rayon de cercle, et autres sur un pied d' égalité avec le périmètre de la circonférence inconnue. Un programme informatique simple pour les constructions géométriques trouver des zones et des périmètres de la circonférence n'a pas été trouvé.
Nous supposons l'existence de preuves sans rayon de cercle. Examinons cela dans les promenades et les différends mathématiques, et pratiquement prouver qu'il est encore un cercle, ou plutôt la capacité de faire tourner la roue.
Version imprimable
Auteur: Elman Jamilov
PS matériau est protégé.
Date de publication 02.25.2004gg




Commentaires
Commentant, gardez à l' esprit que le contenu et le ton de vos messages peuvent blesser les sentiments des gens réels, montrer du respect et de la tolérance à ses interlocuteurs, même si vous ne partagez pas leur avis, votre comportement en termes de liberté d'expression et de l' anonymat offert par Internet, est en train de changer non seulement virtuel, mais dans le monde réel. Tous les commentaires sont cachés à l'index, le contrôle anti - spam.