| section Accueil
Production, Amateur Radio amateur avions de modèle, fusée Utile, divertissant |
maître furtif
électronique physique de la technologie invention |
espace Mystery
Mystères de la Terre Secrets de l'océan infiltration section Carte |
|
| Utilisation de matériel est autorisé à titre de référence (pour les sites - hyperliens) | |||
Navigation: => |
Accueil / Physique / Expérience / |
|
Sur la possibilité de déplacer système mécanique
En raison de forces internes
![]()
Laisser un commentaire

L'auteur arrive avec les nouvelles lois et en tout cas
Il ne tente pas de couper le courant.
Est-il possible de déplacer le système mécanique fermé, qui ne sont pas soumis à des forces extérieures?
Il y a un théorème sur le nombre de mouvements:
La dérivée temporelle de la quantité de vecteur de mouvement d'un système est le principal vecteur de toutes les forces extérieures agissant sur le système.
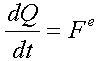
Ce théorème implique plusieurs conséquences:
- Les forces internes affectent pas directement la variation de la quantité de mouvement du système.
- Si le vecteur principal de toutes les forces extérieures agissant sur le système est égal à zéro, le nombre de mouvements de vecteur matériel du système reste constante en amplitude et en direction.
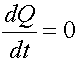
- Si la projection du vecteur résultant des forces extérieures appliquées au système par un certain axe fixe est égal à zéro, alors la projection de la quantité de mouvement du système reste constante sur cet axe.
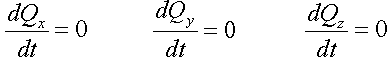
Conséquences (2.3), en effet, appelé la loi de conservation de l' élan.
Pour un système fermé, qui est, le système ne subit pas d'influences extérieures, ou dans le cas où la force nette sur le système géométrique des forces extérieures est égale à zéro, il existe une loi de conservation du moment.
Le nombre de pièces en mouvement du système (par exemple, sous l'influence des forces internes) peut varier, mais de telle sorte que la quantité
![]() reste constante.
reste constante.
La loi de conservation de l'impulsion ne peut être rompu. Impossible!
Et il ne peut pas être contourné.
Et si vous ne pouvez pas l'utiliser pour résoudre le problème, à première vue, contraire à la loi?
J'attirer votre attention sur le schéma suivant de l'argument:
La figure 1 montre le corps de déplacement ne peut être effectué sans que le processus dans l'autre corps.
Etant donné que la quantité de mouvement du corps dans la projection sur les axes de coordonnées, varie de façon continue et diffère de zéro.
Fig.1
Interconnecté et inséparable connexion corps non étirable peut être déplacé comme illustré dans Fig.2.
Avec ce mouvement, le corps se déplace dans un cercle dont le rayon est inversement proportionnelle à leurs masses.
Ce - une conséquence de la loi de conservation de l'élan.
Dans ce cas, l'impulsion totale du système est nulle.
Fig.2
Voici comment cela se pencherait sur le cas de deux objets «réels» (figure 3).
Nous appelons l'un d'entre eux "corps", et un autre - "fluide de travail" ou "substance de travail".
Figure 3
Si le mouvement relatif (autour) du boîtier participent deux corps de travail (ayant la même masse et la vitesse de déplacement relatif) (figure 4), dans un tel cas, le corps obtient un mouvement de rotation.
Dans ce cas, l'impulsion totale des deux fluides de travail dans la projection sur l'axe X est égal à zéro.
Par conséquent, l'organe d'impulsion, dans la projection sur le même axe, de manière à être égale à zéro.
Le cas sera un mouvement alternatif par rapport au centre de masse du système de corps entier.
Déplacer le corps sera effectuée le long d'un axe du "absolu", d'un système de coordonnées fixe.
Dans le système de coordonnées associé au corps, le corps de travail se déplaçant dans un cercle.
Dans le système de coordonnées fixe, les organes de travail se déplacent sur un trajet elliptique.
Rendre l'énergie cinétique des composants mécaniques du système est rendu possible grâce à la conversion d'autres types d'énergie inclus dans le système fermé.
Cela est, d'organiser les mouvements relatifs des composants du système peut être dû à des forces internes.
Dans ce cas, le centre de masse de l'ensemble du système restera toujours en place, qui est, ne pas changer ses coordonnées (ou déplacer uniformément).
Figure 4
On modifie le système représenté sur la figure 1.
Nous n'utilisons "point" le corps et uniformément répartie, à un certain stade de la trajectoire, les masses ouvrières (Figure 5).
Figure 5
Avec un mouvement relatif uniforme entre «corps» et les «masses laborieuses» se déplace dans un cercle dont le rayon est inversement proportionnelle à leur masse (figure 6). Sous le rayon de la trajectoire des masses laborieuses ont besoin de comprendre le rayon de la trajectoire du centre de masse (CM) des masses laborieuses (le point rouge sur la figure).
Figure 6
Voici à quoi il ressemblerait un système de téléphone «réel». (Figure 7)
Figure 7
De la même façon (figure 4), peut être utilisé dans le système d'un certain nombre de masses de travail pour équilibrer le moment angulaire. (Figure 8)
Encore une fois, le centre de masse du système est fixe.
Figure 8
Et ce qui se passe si les masses laborieuses seront uniformément et intimement remplir le chemin de l' ensemble du Voyage? (Figure 9) Rien! Le centre de gravité des masses de travail coïncide avec le centre de masse du corps. La dynamique totale des masses de travail réparties dans une projection sur tous les axes est nul. Par conséquent, l'impulsion zéro et le boîtier.
Les centres de masse des composants du système ne sont pas déplacés par rapport à l'autre. La stabilité du système est stationnaire. Dans le même temps, nous pouvons passer à la masse en mouvement de l'énergie cinétique considérable de travail.
Figure 9
commence "intéressants" quand on commence à arrêter de bouger les masses laborieuses à un certain point de la trajectoire. (Figure 10)
Stop - ce qui signifie, dans ce cas, - consécutive "composé" de toutes les particules élémentaires de la masse de travail avec le boîtier.
Autrement dit, les particules des masses laborieuses à un certain point de la trajectoire gagnent toujours le corps de la vitesse, de perdre la vitesse relative du mouvement. Dans le même temps, le reste des masses laborieuses continue de se déplacer jusqu'à ce que toutes ses particules n'acquièrent la vitesse du corps.
Par exemple, le déplacement du fluide le long d'un certain chemin fermé, on commence brusquement à le recueillir dans un récipient qui est monté de manière fixe dans le boîtier.
Figure 10
Dans la figure animée CM conditionnelle des masses ouvrières est marquée en rouge. Vert - la trajectoire de déplacement de la CM dans son mouvement relatif par rapport à «l'organisme."
Déplacement du vecteur de rayon de la CM des masses laborieuses peut être considéré comme le mouvement d'un pendule avec une masse variable et une longueur variable. (Dans le système de coordonnées associé au corps).
Ici et décidé un défi intéressant:
- calculer comment déplacer les composants du système?
Les calculs ont conduit au résultat suivant (figure 11).
Après l'achèvement de l'ensemble du cycle de travail de masses d'arrêt CM de l'ensemble du système est décalée par rapport à sa position initiale. Le système se déplace conformément à la loi de conservation de l' élan!
Vous pourriez dire différemment: Afin de mettre en œuvre la loi de conservation de l' impulsion, le centre de masse du système mécanique est nécessaire de se déplacer.
Le premier calcul est effectué sur la base de la loi de conservation de l' élan.
La seconde - avec l'aide des équations de Lagrange de type II.
Les résultats sont les mêmes.
Pour résoudre ce problème complètement pas considéré comme une interaction interne des composants du système.
Aucune collision!
Il n'y a pas de forces d'inertie!
Seule l'énergie cinétique et de l'état du système.
Figure 11
Figure 11 ajouté à la finale, troisième étape - la réduction des centres de logement de masse et les masses ouvrières en un seul endroit. Il est nécessaire pour une représentation plus visuelle de la totalité du cycle de mouvement, avec possibilité de répétition de ce cycle. La ligne rouge sur la figure représente le chemin du CM de l'ensemble du système, bleu - boîtier CM.
Les calculs mathématiques, décrivant ce phénomène est attendu, vous pouvez jeter un oeil à l'adresse suivante: http://varipend.narod.ru
Version imprimable
Auteur: Sergej Butov
PS matériau est protégé.
Date de publication 23.12.2006gg




Commentaires
Commentant, gardez à l' esprit que le contenu et le ton de vos messages peuvent blesser les sentiments des gens réels, montrer du respect et de la tolérance à ses interlocuteurs, même si vous ne partagez pas leur avis, votre comportement en termes de liberté d'expression et de l' anonymat offert par Internet, est en train de changer non seulement virtuel, mais dans le monde réel. Tous les commentaires sont cachés à l'index, le contrôle anti - spam.