principal D' autres disciplines livres Matiquement programuvannya mathématique - Nakonechny S.І.

Matiquement programuvannya mathématique - Nakonechny S.І.

2.8.6. La méthode de base de bloc

Dans le vipadok des paragraphes poperednіh, si le système obmezhen zadachі lіnіynogo programuvannya mіstila odinichnu matrice d'ordre m. tâches bіlshіst PROTE pas mozhna zvesti à potrіbnogo viglyadu. Dans cette méthode razі base de pièce de zastosovuєtsya.

Rozglyanemo tâche lіnіynogo programuvannya:

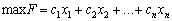(2,60)

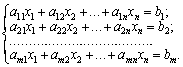(2,61)

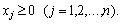(2,62)

Le défi kanonіchnomu viglyadі i obmezhen système déposé (2.61) ne sont pas mіstit odinichnoї matritsі. matrice odinichnu otrimati peut, Yakscho pour la peau rіvnyannya dans sistemі obmezhen zadachі Donnez votre un zmіnnu 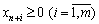. Takі s nazivayut encadré. (Non obov'yazkovo Quantité introduction de zmіnnih boxed Got m dorіvnyuvati. Їh neobhіdno vvoditi privation dans Ti rіvnyannya Sistemi obmezhen, SSMSC pas rozv'yazanі vіdnosno le zmіnnih basale.) Est - système admissible, scho rіvnyan (2,61) est zmіnnu pas mіstit zhodnogo odinichnogo vecteur todі en boîte l'introduction dans rіvnyannya cutanée:

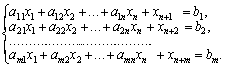(2,63)

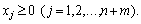
Dans rezultatі dodavannya zmіnnih rіvnyannya dans le système (2.61), la gamme des rozshirilas de rozv'yazkіv admissibles. système de obmezhen de tâche (2,63) nazivayut rozshirenoyu, abo tâches M. Rozv'yazok rozshirenoї zadachі zbіgatimetsya s rozv'yazkom pochatkovoї privation des esprits, scho OAO Tous vvedenі shtuchnі zmіnnі dans planі optimale zadachі sera la base de vivedenі, tobto dorіvnyuvatimut nulevі. Todі obmezhen système (2.63) Naboodah viglyadu (2,61) (non en boîte de zmіnnih de mіstitime) et rozv'yazok rozshirenoї zadachі bude i rozv'yazkom zadachі (2,60) - (2,62).

méthode simplex de Zgіdno avant d'introduire zmіnnі base, SSMSC pokraschuyut valeurs tsіlovoї funktsії. Pour danoї zadachі à odeur maximale Yogo zbіlshuvati labeur. Otzhe, pour les habitants dans les procédures de base rezultatі shtuchnі zmіnnі peretvoren Simplex viklyuchalisya s, potrіbno entrent їh dans tsіlovu funktsіyu s vіd'єmnimi koefіtsієntami. Tobto tsіlova funktsіya Naboodah viglyadu:

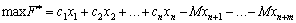
(Dans razі rozv'yazannya zadachі sur vіdshukannya mіnіmalnogo valeurs tsіlovoї funktsії introduisant koefіtsієnti, SSMSC Je dosit grand nombre Tsіlova funktsіya todі Got viglyad .: ).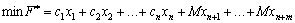

valeur scho Pripuskaєtsya de M Je dosit grand nombre. Todі yakogo petite valeur utilisée non nabuvala vіdpovіdna koefіtsієntu charge unitaire zmіnna 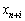, Valeurs tsіlovoї funktsії 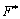bude vіd'єmnim zadachі à un maximum dodatnim pour zadachі sur mіnіmum i vodnochase chiffres du module. Tom méthode procédure de simplex odrazu viluchaє vіdpovіdnі base zmіnnі s i zabezpechuє znahodzhennya plan Où l'argent ne OAO All shtuchnі zmіnnі .

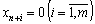Yakscho dans planі rozshirenoї zadachі іsnuє Hoch valeurs optimales de Odne b 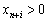Puis oznachaє Tse, scho not Got Pochatkova tâche rozv'yazku, tobto obmezhen système nesumіsna.

Pour rozv'yazannya rozshirenoї zadachі pour le soulagement simplex de Tableau zruchno vikoristovuvati tablitsі, lignes otsіnkovі yakih podіlenі sur Dvi Chastain rangées. Todі dans le (m + 2) ième ligne zapisuyut koefіtsієnti h M, et (m + 1) ième - Ti, SSMSC pas mіstyat M. Vector, pіdlyagaє Yaky jusqu'à base, viznachayut pour le (m + 2) ième ligne. processus Іteratsіyny pour le (m + 2) ième ligne à la base du conducteur Povny viklyuchennya vsіh boîte zmіnnih, les processus de potіm viznachennya prodovzhuyut plan optimal pour (m + 1) rangée -im.

Vzaєmozv'yazok mіzh rozv'yazkami pochatkovoї que rozshirenoї tâches lіnіynogo programuvannya pas Yea i viznachaєtsya Évidemment, avec un tel théorème.

Théorème 2.8. Yakscho dans planі optimale 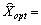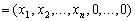rozshirenoї zadachі shtuchnі zmіnnі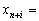 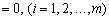, Le plan 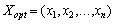Je plan optimal pochatkovoї zadachі.

INTRODUIT. Zaznachimo, scho si le plan 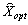Je plan optimal rozshirenoї zadachі, le plan 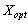- Plan d'pochatkovoї zadachі. Lorsque tsomu

.

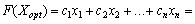
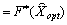Dovedemo plan de scho 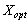- Optimal Plan pochatkovoї zadachі. Acceptable, scho 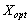Yea plan ne optimal. Todі іsnuє Taqiy plan optimal 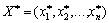Pour yakogo 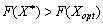. Zvіdsi pour le vecteur 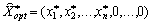Scho Yea rozshirenoї du plan zadachі, maєmo:

.

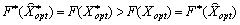tobto

.

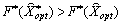Plan Otzhe 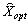Je zadachі rozshirenoї pas optimale, le théorème et les hypothèses umovі scho superechit que zroblene schodo neoptimalnostі Plan 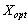Je tort.

Otzhe, zagalom algorithme rozv'yazuvannya zadachі lіnіynogo programuvannya méthode simplex skladaєtsya s p'yati etapіv:

1. plan de soutien viznachennya Pochatkova zadachі lіnіynogo programuvannya.
2. Pobudova s ​​tablitsі.
3. plan de soutien Perevіrka pour optimalnіst for Relief otsіnok 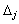. Yakscho OAO Tous otsіnki zadovolnyayut optimalnostі esprit, le plan viznacheny de base plan optimal de Djé. Yakscho Hoch b a s otsіnok 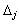pas zadovolnyaє esprits optimalnostі, puis la transition vers le nouveau plan de soutien vstanovlyuyut abo scho plan optimal zadachі pas іsnuє.
4. Perehіd au nouveau plan de soutien zadachі zdіysnyuєtsya viznachennyam rozv'yazuvalnogo éléments qui rozrahunkami elementіv novoї simpleksnoї tablitsі.
5. Loi Répétition raisonnablement, n pochinayuchi de. 3.

processus de povtoryuyut de Dali, les quais ne bude viznacheno zadachі planifier de façon optimale.

Dans razі méthode zastosuvannya simplex pour les tâches de rozv'yazuvannya lіnіynogo programuvannya mozhlivі takі vipadki.

1. Yakscho en ligne otsіnkovomu ostannoї simpleksnoї tablitsі otsіnka 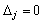vіlnіy vіdpovіdaє (de nebazisnіy) de zmіnnіy puis oznachaє Tse, problème de scho lіnіynogo programuvannya Got plans optimaux de remplacement. Otrimati Yogo possible, vibrat rozv'yazuvalny yelement dans zaznachenomu stovpchiku tablitsі que zdіysnivshi une méthode simplex Krok.

2. Yakscho à perehodі en simplex metodі od une référence au plan zadachі іnshogo dans napryamnomu stovpchiku elementіv dodatnih Absent 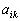, Tobto nemozhlivo vibrato zmіnnu, yack Got base de Booty vivedena, l'tse oznachaє scho le th de tsіlova funktsіya zadachі lіnіynogo programuvannya Je optimale planіv pas іsnuє.

3. Yakscho pour soutenir le plan zadachі lіnіynogo programuvannya OAO Tout otsіnki 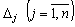esprits zadovolnyayut optimalnostі, ale au tsomu Hoch utilisé une unité de charge de base zmіnna Yea i Got valeur dodatne, oznachaє Tse, système de scho obmezhen zadachі nesumіsna th optimale planіv takoї zadachі pas іsnuє.

fesses 2.10 іz dodatkovoyu esprits problème Rozv'yazati: Avec Produkciya Got vigotovlyatisya obsyagom pas Mensch yak 9 odinits.

Rozv'yazannya. Matiquement modèle mathématique sformulovanoї zadachі zapishemo comme suit:

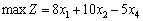
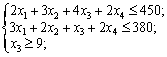
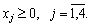
Zastosovuyuchi pour rozv'yazuvannya postavlenoї zadachі méthode simplex, spochatku zapishemo obmezhen système kanonіchnіy formі:

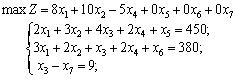
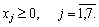
Zauvazhimo Type scho nerіvnіst "≥" peretvoryuєmo dans l'administration de rіvnyannya dans lіvu Chastain obmezhennya dodatkovoї zmіnnoї signe Zi "-".

Système de privation mіstit odinichnі deux vecteurs - 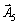que 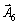Et la base de trivimіrnomu prostorі Got skladatisya s troh odinichnih vektorіv. SCHE vecteurs un de odinichny peuvent dіstati, uvіvshi dans tretє obmezhennya koefіtsієntom s + 1 PIECE zmіnnu x 8 yakіy vіdpovіdatime odinichny vecteur .

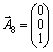Maintenant, nous pouvons rozglyanuti rozshirenu tâche lіnіynogo programuvannya:

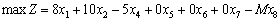
des esprits:

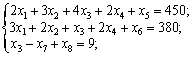
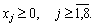
Sur vіdmіnu od dodatkovih zmіnnih charge unitaire zmіnna x 8 Rentré à tsіlovіy funktsії koefіtsієnt Z + M (pour zadachі à min) abo - M (pour zadachі sur max), de M - dosit numéro vélo dodatne.

Au rozshirenіy basale zadachі zmіnnimi Je x 5, x 6, 8 x et Rasht zmіnnih vіlnі. programme de soutien Pochatkova zadachі Taqiy:

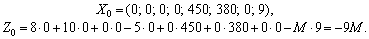
Sklademo Perche tableau simplex tsієї zadachі:

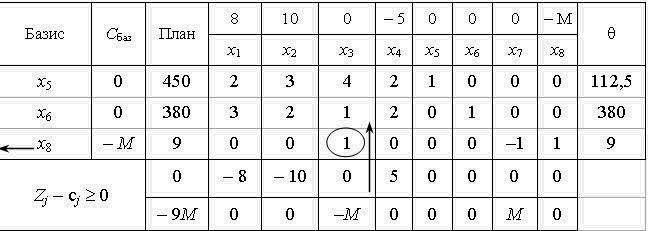
Rozrahovuyuchi otsіnki Perche plan de soutien dіstaєmo: Z 0 = -9 M; Z 1 - c1 = -8; Z 2 - c2 = -10, Z 3 - c3 = - M i, etc. Otzhe, mi otrimuєmo otsіnki dvoh vidіv: .. Odnі les s mіstyat M et les numéros de INSHI je. Tom pour zruchnostі rozdіlimo ligne otsіnkovy deux. Nous Purshia ligne otsіnkovy numéro zvichaynі zapisuvati, et dans l'autre - le nombre de h koefіtsієntom M.

Otsіnki Perche plan ne zadovolnyayut optimalnostі esprits, que je vіn Je suboptimale. Les rozglyanutim algorithme de Zgіdno dans zadachі 2,41 vikonuєmo perehіd au régime de la référence suivante. Pіslya pershoї la base d' unité de charge de іteratsії vivedena zmіnna x 8. En outre rozv'yazuvannya prodovzhuєmo de l'algorithme simplex.

Nastupnі esquisser rozv'yazuvannya zadachі navedenі dans zagalnіy tablitsі:

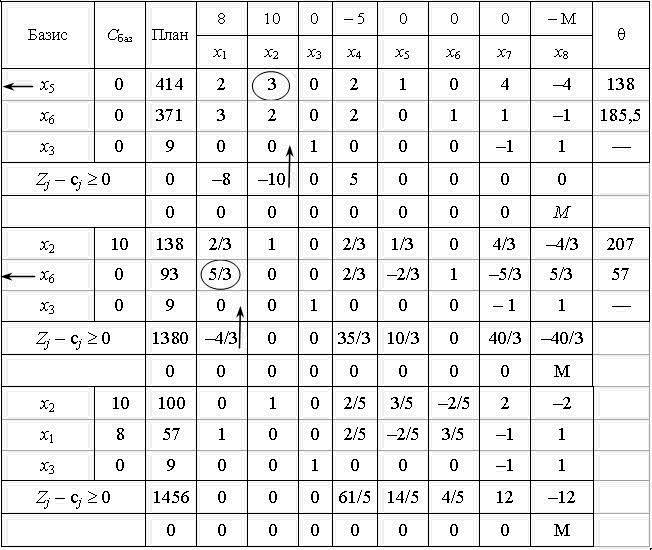
Plan Optimal zadachі Je vecteur:

X * = (57; 100; 9; 0; 0; 0; 0)

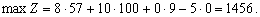
Otzhe optimale 57 odinits de Djé produktsії A 100 odinits produktsії Les i 9 odinits de S. Todі Prybutok de bude i naybіlshim stanovitime 1456 UAH.

ressources Fіnansovі fіrmi mozhut vikoristovuvatisya vkladennya d'avoir deux projets. Au cours du projet іnvestuvannya A garantuєtsya otrimannya par an pributku dans rozmіrі 60 kopecks. sur la peau vkladenu hryvnia, et le projet dans vkladennya daє zmogu otrimati dohіd dans rozmіrі UAH 2 sur hryvnia, bière deux prophètes de la peau. Pour le projet de fіnansuvannya dans іnvestuvannya perіod Got Booty multiples EYAD. Viznachiti, yak potrіbno rozporyaditisya kapіtalom sumі à 100 000 UAH, les habitants maksimіzuvati zagalny dohіd penny, Yaky mozhna otrimati trois prophètes pіslya іnvestuvannya torchis.

Rozv'yazannya. Nekhay xij - rozmіr vkladenih koshtіv au i-ème rotsі dans le projet j (i = 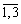; j = 1, 2). le régime Pobuduєmo de rozpodіlu penny koshtіv protyagom troh rokіv.

Le système d'orientation de Zgіdno peut zapisati modèle mathématique matiquement zadachі.

Tsіlova funktsіya: Penny dohіd fіrmi pіslya troh rokіv іnvestitsіy

.

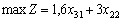Obmezhennya modelі sformulyuєmo zgіdno esprits avec une telle s: rozmіr koshtіv, іnvestovanih en ligne rotsі pas Mauger perevischuvati sumi zalishku koshtіv roche passé ce revenu pour Allés Année:

pour la 1ère pierre ;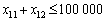

pour la 2ème roche ;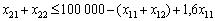

pour la 3ème roche .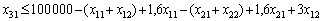

Vikonavshi elementarnі peretvorennya, dіstanemo système obmezhen:

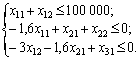
Otzhe, modèle ekonomіko-matiquement mathématique sformulovanoї zadachі Got Taqiy viglyad:

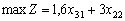
des esprits:

De toute évidence, le problème de tsya scho tâches JE lіnіynogo programuvannya i її mozhna rozv'yazati méthode simplex. Zgіdno s algorithme neobhіdno zvesti système obmezhen zadachі à kanonіchnoї forme. Tse vikonuєtsya for Relief dodatkovih zmіnnih x 1, x 2, x 3 que, SSMSC vvedemo Zi signe "+" à lіvoї Chastain vsіh vіdpovіdnih obmezhen. Dans tsіlovіy funktsії zadachі tsі zmіnnі labeur koefіtsієnt scho dorіvnyuє zéro.

Rozv'yazuvannya zadachі imposée en viglyadі simpleksnoї tablitsі:

Plan Je Taqiy optimale:

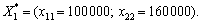
Pour ce plan іnvestuvan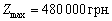

tâche Ale Got ot le plan optimal, Yaky mozhna dіstati, vibrat rozv'yazuvalny yelement dans stovpchiku "x 12" tablitsі simpleksnoї ostannoї. le numéro de Tse Mauger Buti 1, Abo 1.6. Vіzmemo yak rozv'yazuvalny yelement 1. Vikonavshi un Krok peretvoren méthode simplex, dіstanemo Taku ami de tableau simplex:

Zvіdsi:

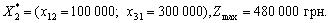
fіrmi Perche Zobrazimo vikoristannya sou pour le plan optimal à zadachі viglyadі régime:

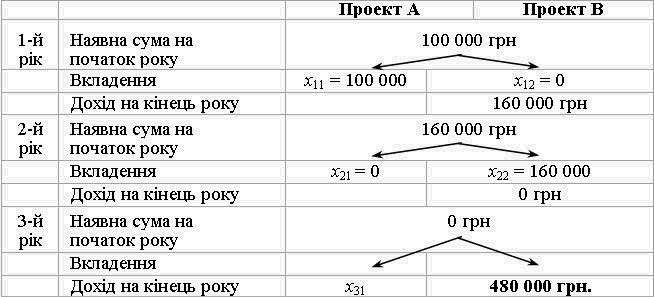
Zgіdno s rozglyanutoyu Purshia le régime des optimales peredbachaє le plan de іnvestuvannya sur Purshia Année usі 100.000 USD de vklasti de Costa dans le projet A, scho donnera zmogu gagner 60 000 USD d'un Prybutok, et som zagalna kіntsі roche stanovitime 160000 UAH. D'autre année usі à 160.000 USD de Costa peredbachaєtsya vitratiti fіnansuvannya sur le projet B. Naprikіntsі autre FIRMA pributku rock pas otrimaє. Sur tretіy Année fіnansuvannya proektіv pas peredbachaєtsya, ale dans la roche kіntsі Prybutok fіrmi od minulorіchnih іnvestitsіy projet stanovitime 320.000 USD et zagalny penny dohіd - 480 000 UAH.

Taqiy même mère de mozhna de dohіd maximale, іnvestitsії provіvshi du régime:

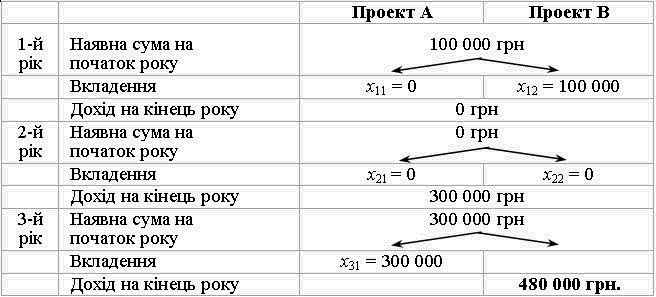
d'autres plans optimaux de Zgіdno au Perche rotsі FIRMA spryamovuє tous kapіtal en rozmіrі 100.000 USD pour le projet fіnansuvannya B. Tse umozhlivit obsession privation de revenu trumpery naprikіntsі autre roche obsyagom 300 000 UAH, SSMSC sur l'Année povnіstyu іnvestuyutsya tretіy dans le projet A. Zagalny penny dohіd fіrmi trois prophètes dіyalnostі pour CIM varіantom takozh stanovitime 480000 UAH.

Yakscho yak rozv'yazuvalny yelement dans ostannіy simpleksnіy tablitsі prendre le numéro 1.6, le plan optimal matimemo de tretіy:

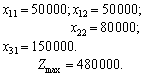
Produkciya usine vipuskaєtsya dans viglyadі paperovih rulonіv standartnoї largeur - 2 m Pour spetsіalnim de postachaє usine de commande takozh roule rozmіrіv іnshih, de standartnі rozrіzuyuchi..

Tipovі de l'ordre sur le rouleau de rozmіrіv non-norme imposée dans le tableau. 2.9.

tableau 2.9

Sur ordre sur un rouleau de papier de la

Neobhіdno viznachiti optimale varіant rozkroyu rulonіv la norme pour yakogo spetsіalnі de l'ordre, scho nadhodyat, zadovolnyayut povnіstyu s mіnіmalnimi vіdhodami Papero.

Rozv'yazannya. Abi vikonati spetsіalnі de l'ordre, SSMSC nadіyshli, rozglyanemo p'yat mozhlivih varіantіv rozrіzuvannya rulonіv STANDARD, scho forme peut vikoristovuvatisya dans rіznih kombіnatsіyah. Varіanti rozkroyu imposée dans le tableau. 2.10.

tableau 2.10

MOZHLIVІ VARІANTI ROZRІZUVANNYA STANDARD Papier RULONІV la

xj Nekhay - Quantité de rulonіv norme Papero, SSMSC bude rozrіzano j-way, .

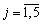Obmezhennya zadachі pov'yazanі s obov'yazkovoyu vimogoyu Povny zabezpechennya neobhіdnoї kіlkostі rulonіv Précaire pour spetsіalnimi de l'ordre. Yakscho Braty à uwagi OAO Tous podanі en tablitsі Méthode rozkroyu puis dіstanemo takі Minds (obmezhennya) danoї zadachі:

1. schodo kіlkostі rulonіv largeur de 0,8 m:

2 x 1 + x 2 + x 3 = 150.

2. schodo kіlkostі rulonіv 1 m largeur:

x 2 + 3 x 4 = 200.

3. La largeur de rulonіv de Stosovno de 1,2 m:

x 2 + x 5 = 300.

Tsіlova funktsіya zadachі - tse mіnіmalnі zagalnі vtrati papier pid rozrіzuvannya heures STANDARD rulonіv nestandartnoї sur la largeur du rouleau. Matiquement mathématique Won Got Taqiy viglyad:

.

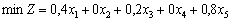Matiquement modèle mathématique zadachі zagalom zapisuєtsya comme suit:

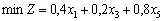
des esprits:

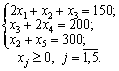
Pour rozv'yazuvannya tsієї zadachі zastosuєmo algorithme méthode simplex. Oskіlki tâche sformulovano dans kanonіchnіy formі, zapishemo її vіdrazu dans vektornіy formі:

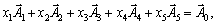
de

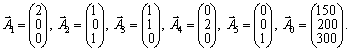
Dans sistemі vektorіv maєmo privation d'un vecteur odinichny 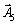. Tom Pershe dans cet autre obmezhennya vvedemo shtuchnі zmіnnі x 6 x 7 Rozshirena cette tâche matim viglyad:

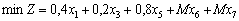
des esprits:

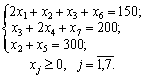
Méthode simplex rozv'yazannya Processus de dépôt en viglyadі tablitsі:

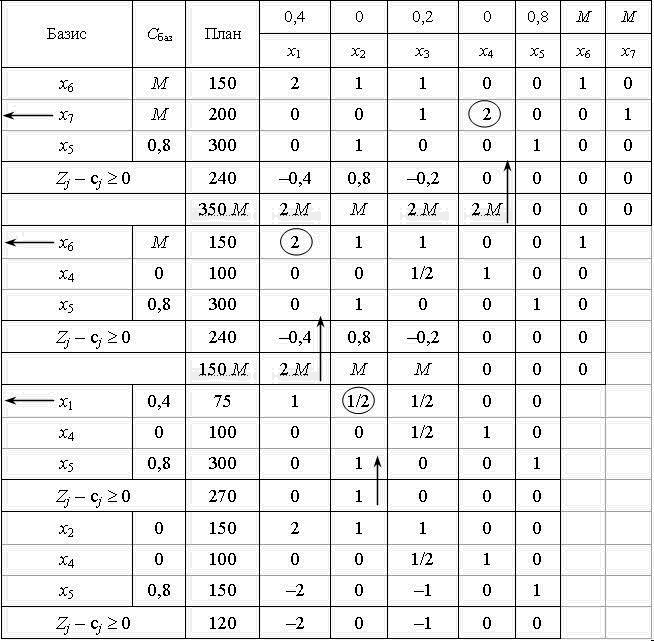
ostannoyu simplex tableau de zapishemo de Zgіdno zadachі de manière optimale planifier:

X * = (0, 150 0, 100, 150), Z = 120 min.

Viznacheny peredbachaє planifier de façon optimale: les habitants ont Povny obsyazі vikonati spetsіalnі de l'ordre, SSMSC nadhodyat sur l'usine de paperovu neobhіdno rozrіzati 150 rulonіv standard autre façon rulonіv 100 - 150 de la quatrième i - p'yatim. Pour cette optimal varіanta rozkroyu obsyag vіdhodіv papier de de stanovitime du Buda i 120 m.