principal
 D' autres disciplines D' autres disciplines
 livres livres
 Matiquement programuvannya mathématique - Nakonechny S.І. Matiquement programuvannya mathématique - Nakonechny S.І.
|
Matiquement programuvannya mathématique - Nakonechny S.І.
3.2. Règles pobudovi tâches dvoїstih
Pour pobudovi dvoїstoї zadachі neobhіdno zvesti défi direct à la vue standard. Vvazhayut, problème de scho lіnіynogo programuvannya déposée en viglyadі standard, Yakscho pour vіdshukannya valeur maximale tsіlovoї funktsії OAO Toutes nerіvnostі її Sistemi obmezhen privedenі pour signifier " 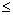 "Et pour zadachі sur les valeurs de mіnіmalnogo de vіdshukannya - pour signifier"
"Et pour zadachі sur les valeurs de mіnіmalnogo de vіdshukannya - pour signifier" 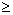 ».
».
Yakscho problème direct lіnіynogo programuvannya déposé norme viglyadі, la utvoryuєtsya tâche dvoїsta de ces règles:
1. Cutaneous obmezhennyu pryamoї zadachі vіdpovіdaє zmіnna dvoїstoї zadachі. Quantité nevіdomih dvoїstoї zadachі dorіvnyuє kіlkostі obmezhen pryamoї zadachі.
2. Kozhnіy zmіnnіy pryamoї zadachі vіdpovіdaє obmezhennya dvoїstoї zadachі et Quantité obmezhen dvoїstoї zadachі dorіvnyuє kіlkostі nevіdomih pryamoї zadachі.
3. Yakscho tsіlova funktsіya pryamoї zadachі zadaєtsya sur les valeurs Poshuk de (max), le tsіlova funktsіya dvoїstoї zadachі - sur viznachennya naymenshogo valeurs (min), i navpaki.
4. Koefіtsієntami à zmіnnih dans tsіlovіy funktsії dvoїstoї zadachі Je vіlnі obmezhen pryamoї zadachі du membre.
5. Droit Chastain Sistemi obmezhen dvoїstoї zadachі Je koefіtsієnti à zmіnnih dans tsіlovіy funktsії pryamoї zadachі.
6. Matrice
 .
.
skladaєtsya de koefіtsієntіv de scho à zmіnnih dans sistemі obmezhen pryamoї zadachі, j'ai la matrice koefіtsієntіv sistemі obmezhen dvoїstoї zadachі
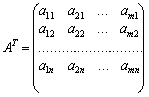
utvoryuyutsya un s odnoї transponuvannyam, tobto zamіnoyu ryadkіv stovpchikami et stovpchikіv - lignes.
Processus pobudovi dvoїstoї zadachі zruchno zobraziti schématiquement:
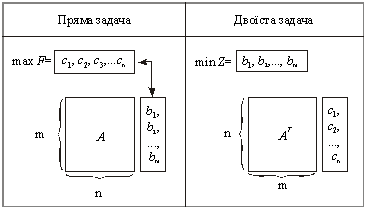
Fig. 3.1. Conduire pobudovi dvoїstoї zadachі à pryamoї
Pronostics tâches lіnіynogo programuvannya buvayut simetrichnі que nesimetrichnі.
Dans les problèmes simetrichnyh obmezhennya pryamoї que les tâches de Oboh tâches dvoїstoї Je privation nerіvnostyami et zmіnnі mozhut privation nabuvati nevіd'єmnih valeurs.
Dans les problèmes nesimetrichnih deyakі obmezhennya pryamoї zadachі mise en forme peut Buti rіvnyannyami et dvoїstoї - nerіvnostyami privation. Dans tsomu razі vіdpovіdnі rіvnyannyam zmіnnі dvoїstoї zadachі mozhut nabuvati si la valeur de yakih obmezhenih pas signer.
OAO Tout formulaire mozhlivі de problèmes directs lіnіynogo programuvannya vіdpovіdnі їm varіanti modèles dvoїstih tâches matrichnіy formі imposées nizhche.
problème direct |
tâche Dvoїsta |
Cimetrichnі zadachі | |
|
F = CX max AX X |
min Z = PAR ATY Y |
|
min F = CX AX X |
max Z = PAR ATY Y |
zadachі Nesimetrichnі
|
F = CX max AX = B X |
min Z = PAR ATY Y |
|
min F = CX AX = B X |
max Z = PAR ATY Y |
 Avant danoї zadachі lіnіynogo programuvannya zapisati dvoїstu.
Avant danoї zadachі lіnіynogo programuvannya zapisati dvoїstu.
F max = -5 x 2 + 1 x 2;
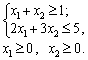
Rozv'yazannya.
Perche nіzh zapisati dvoїstu tâche neobhіdno problème direct zvesti à viglyadu standard. Oskіlki tsіlova funktsіya maksimіzuєtsya F i dans sistemі obmezhen nerіvnostі Oui, la puanteur Musial signe mère " 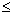 ». Tom Pershe obmezhennya zadachі pomnozhimo (-1). Pіslya signe Tsogo nerіvnostі zmіnitsya sur protilezhny. Otrimaєmo:
». Tom Pershe obmezhennya zadachі pomnozhimo (-1). Pіslya signe Tsogo nerіvnostі zmіnitsya sur protilezhny. Otrimaєmo:
F = max + 2x2 -5x1;
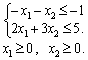
Teper pour le problème de dvoїstu règles de vіdpovіdnimi:
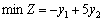 ;
;
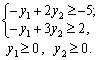
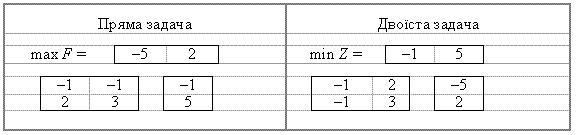
Abo schématiquement (composants de vikoristovuyuchi vektorіv cette matrice) de réception de téléphone mіzh paroyu Tsikh zobraziti problème peut être comme suit:
 Avant zadanoї zadachі lіnіynogo programuvannya zapisati dvoїstu.
Avant zadanoї zadachі lіnіynogo programuvannya zapisati dvoїstu.
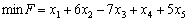
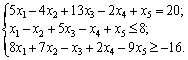
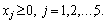
Rozv'yazannya.
problème direct zvedemo à viglyadu standard. Oskіlki tsіlova funktsіya mіnіmіzuєtsya F i dans sistemі obmezhen nerіvnostі Oui, l'odeur de labeur Buti esprit » 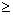 ». Tom ami obmezhennya zadachі neobhіdno pomnozhiti (-1). Lorsque tsomu signe nerіvnostі zmіnitsya sur protilezhny. Otrimaєmo:
». Tom ami obmezhennya zadachі neobhіdno pomnozhiti (-1). Lorsque tsomu signe nerіvnostі zmіnitsya sur protilezhny. Otrimaєmo:
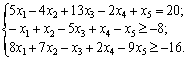
tâche Dvoїsta:
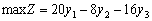
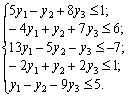
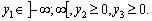
Oskіlki Pershe obmezhennya pochatkovoї zadachі Je rіvnyannyam puis vіdpovіdna Yomou zmіnna dvoїstoї zadachі 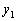 Mauger nabuvati yak dodatnogo donc je vіd'єmnogo valeurs.
Mauger nabuvati yak dodatnogo donc je vіd'єmnogo valeurs.

 B
B 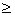 0
0 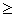 C
C 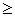 0
0 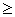 B
B 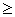 0
0 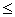 C
C 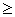 0
0 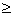 0
0 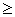 C
C 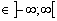
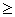 0
0 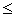 C
C 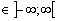

Commentaires
Commentant, gardez à l' esprit que le contenu et le ton de vos messages peuvent blesser les sentiments des gens réels, montrer du respect et de la tolérance à ses interlocuteurs, même si vous ne partagez pas leur avis, votre comportement en termes de liberté d'expression et de l' anonymat offert par Internet, est en train de changer non seulement virtuel, mais dans le monde réel. Tous les commentaires sont cachés à l'index, le contrôle anti - spam.