principal D' autres disciplines livres Matiquement programuvannya mathématique - Nakonechny S.І.

Matiquement programuvannya mathématique - Nakonechny S.І.

3.7.2. Parametrichnі vecteur zmіni koefіtsієntіv tsіlovoї funktsії

Rozglyanemo vipadok lіnіynoї zalezhnostі koefіtsієntіv tsіlovoї funktsії od paramètre valeurs mozhlivі yakogo zadanі neperervnim numérique іntervalom, tobto dans zadachі lіnіynogo programuvannya

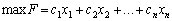(3.80)

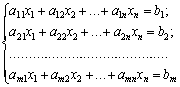(3,81)

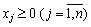(3,82)

scho admissible

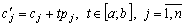. (3,83)

Bien Usі INSHI koefіtsієnti i vіlnі Les membres de quantités d'acier zalishayutsya.

Zapishemo le paramètre ce problème à l'esprit zagalnіy formі:

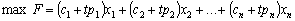(3,84)

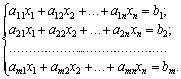(3,85)

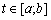
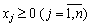. (3,86)

Pour deyakogo valeurs fіksovanogo 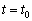problème (3,84) - (3,86) dans la tâche lіnіynogo de programuvannya de peretvoryuєtsya. Zmіni koefіtsієntіv tsіlovoї funktsії dans protsesі realіzatsії méthode simplex à la valeur vplivatimut ligne otsіnkovogo ( ).

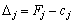Pour le plan optimal zadachі lіnіynogo programuvannya dans postanovtsі (3,36) - (3,38), le § de yak vіdomo 2.7.4, otsіnki vektorіv rozrahovuyut comme suit:

.

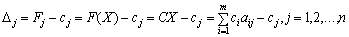Yakscho tsіlova funktsіya Got viglyad (3,84), puis otsіnki vektorіv rozrahovuvatimutsya de la formule:

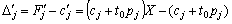
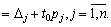
Poznachimo méthode peretvorenі Povny viklyuchen Jordan-Gauss protsesі pererahunku pochatkovoї simpleksnoї tablitsі 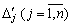par 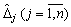, analogіchno 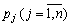- yak 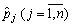. Arrêtez simplex tableau Naboodah tels viglyadu:

tableau 3.6

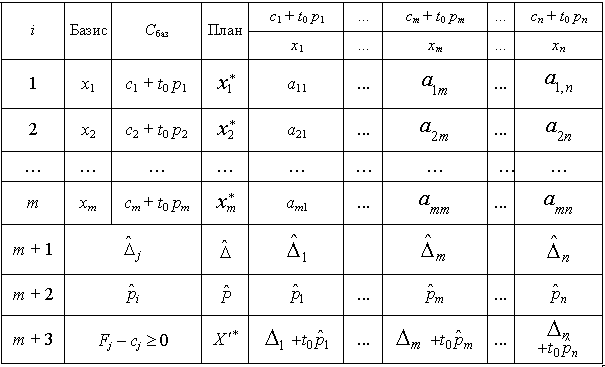
Table (analogіchno vipadku parametrichnoї zmіni vecteur obmezhen -tabl. 3.5) mіstit dodatkovih deux rangées, le stezhiti de daє scho pour les valeurs de peretvorennyami 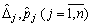pіslya kozhnoї іteratsії.

De toute évidence, problème scho parametrichnoї zmіni vecteur obmezhen Je dvoїstoyu à parametrichnoї vecteur zmіni koefіtsієntіv tsіlovoї funktsії, cela peut être skoristatis algorithme rozv'yazuvannya parametrichnoї zadachі scho imposée dans poperednomu paragrafі.

1. Slіd valeurs deyake zafіksuvati 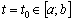i rozv'yazati problème (3,84) - tâche zvichaynu (3,86) de yak lіnіynogo méthode programuvannya simplex.

Le ostannoї de 2. plan optimal simpleksnoї tablitsі 3.6 JE sumoyu dvoh dodankіv, yakih znahodyatsya valeurs dans les lignes que 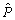Et Got vikonuvatisya Umov nevіd'єmnostі vsіh composante vectorielle scho Yea otsіnkami parametrіv ostannoї simpleksnoї tablitsі, tobto

.

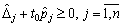3. Vstanovlyuєmo valeur granitsі du paramètre, t, pour le vecteur de yakih 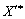zalishatimetsya plan optimal. Pour Tsogo s ostannoї simpleksnoї tablitsі skladaєmo nerіvnostey système

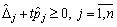. (3,87)

a) Yakscho іsnuyut takі valeurs j, pour yakih 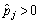, Todі rozv'yazkami vіdpovіdnih nerіvnostey sera:

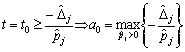. (3,88)

Dans Taqiy sposіb viznachayut bordure inférieure Shukanov іntervalu, yak Mauger dorіvnyuvati et abo Buti Mensch pour neї: .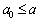

yakscho Absent 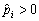, OOO Tout tobto 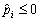, La valeur, t, pour yakih znaydeny 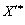bude optimale znizu pas obmezhenі, tobto .

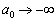b) les valeurs de takі de Yakscho i pour yakih 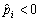Puis rozv'yazkami vіdpovіdnih nerіvnostey sera:

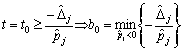. (3,89)

W Tsikh rozv'yazkіv viznachayut limite supérieure Shukanov іntervalu, yak Mauger Buti dorіvnyuvati abo bіlshoyu et ( 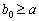). yakscho Absent 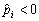, OOO Tout tobto 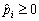valeurs Puis sukupnіst, t, pour le plan de yakih znaydeny 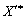bude zverhu optimale neobmezhena ( 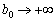) I dans tsomu ostannomu vipadku tâche rozv'yazana povnіstyu, oskіlki

.

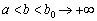4. Le système (3.74) vecteur viznachaє Yaky neobhіdno de Vivest de base. Pripustimo, scho pour deyakogo 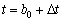de 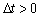, La valeur Mіnіmalne dans (3,89), de yack viznachaє іntervalu limite supérieure 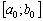, Pour dosyagaєtsya 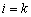. Otzhe, porushuєtsya k -ta nerіvnіst іz (3,87), i s la base neobhіdno vivoditi vecteur scho vіdpovіdaє zmіnnіy 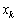. Tom au 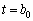neobhіdno dépenser zamіnu base pour Chogo vikonuyut un Krok dvoїstogo méthode simplex rozglyanutogo au § 3.6, i viznachayut base de valeurs .

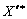Le système de nerіvnostey 5. Rozglyadaєmo de (3.87). pour 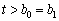de formule (3.77) limite supérieure viznachaєmo 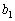Signification calme, t, pour le plan de yakih vіdshukany 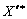bude de façon optimale.

6. La procédure povtoryuєmo Doty, Pokey est pas otrimaєmo valeurs verhnoї granitsі chergovogo іntervalu, scho abo dorіvnyuє perevischuє affectations de limites supérieures іntervalu 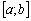mozhlivih valeurs t, tobto

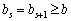. (3,90)

Spіvvіdnoshennya (3,90) i Je Trouve notre ordre, scho problème rozv'yazano.

Otzhe, emplois promіzhok 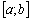podіlyayut un іntervalіv numéro 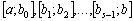Pour yakih le maximum de la peau tsіlovoї funktsії dosyagaєtsya pour vіdpovіdnogo Yomou un plan optimal.

Rozv'yazati la tâche paramètre

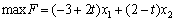
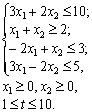
Nekhay 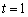. Rozv'yazhemo méthode simplex tâche modifіkovanim, les lignes EYAD dodatkovimi de tables vikoristovuyuchi.

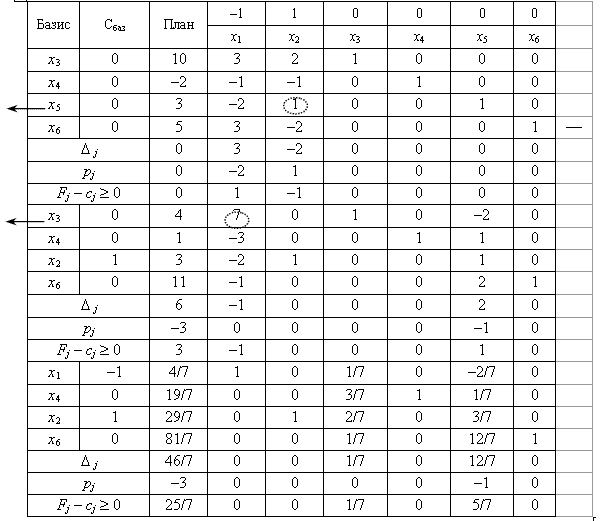
Arrêtez simplex tableau mіstit Purshia de manière optimale planifier zadachі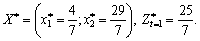

La limite supérieure de zgіdno s Perche promіzhku (3,89) dorіvnyuє 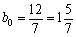. Otzhe sur іntervalі 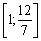plan 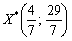bude optimale, la valeur optimale tsіlovoї funktsії bude avec un tel paramètre funktsієyu de lіnіynoyu t:

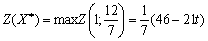
quand je .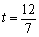

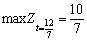Oskіlki à 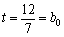yelement m + 2 ligne qui p'yatoї bude nulovim colonne, prenez p'yatu rozv'yazuvalnu colonne pour i, m + 2 rangées vіdkinuvshi, zdіysnyuєmo un іteratsіyu. Table Otrimaєmo taku:

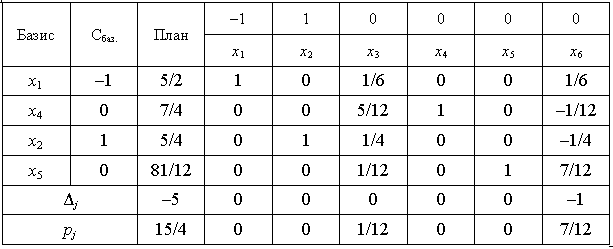
Les m + 3 rangs tsієї tablitsі Absent vіd'єmnih elementіv et zgіdno s formule (3,89) plan de znaydeny 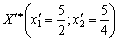bude optimale pour vsіh valeurs t, mensonge scho sur іntervalі 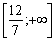. valeur optimale tsіlovoї de funktsієyu de funktsії Je avec un tel paramètre t:

.

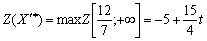à .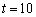

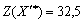Otzhe povnіstyu tâche rozv'yazana.