section Accueil Production, Amateur Radio amateur avions de modèle, fusée Utile, divertissant	maître furtif électronique physique de la technologie invention	espace Mystery Mystères de la Terre Secrets de l'océan infiltration section Carte
Utilisation de matériel est autorisé à titre de référence (pour les sites - hyperliens)

PROPORTIONS DIVINE DE LA SECTION GOLDEN

Bienvenue sur le forum

Si vous venez à un banc vide et asseyez dessus, vous ne restez pas assis au milieu du banc (en quelque sorte impudique, bien qu'il y ait une certaine prononcé) et, bien sûr, pas sur le bord. Si vous tranquillement mesures de longueur sur laquelle son corps a été divisé banc, vous trouverez que plus le rapport entre la longueur et moins bien contre toute la longueur du segment à une plus grande et égale à environ 1,62. Ce nombre est appelé le rapport d'or, une des trois plus grands nombres irrationnels, qui est, ces chiffres, la représentation décimale qui sont infinies et apériodique. Les deux cours autre vous le savez, est p - rapport de la circonférence au diamètre, et e - base des logarithmes naturels (un mot beaucoup n'aiment pas, mais le nombre encore, intéressant). Et, bien que la section d'or et non un mathématiques fondamentales comme l'un de leurs deux, il est important pour notre perception du monde comme une proportion correspondant à la section d'or nous paraissent harmonieux.

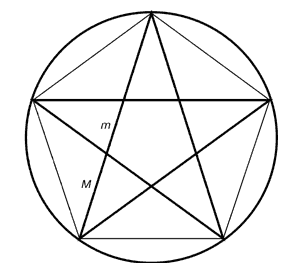
La section d'or était connu des Grecs anciens. Il y a peu de doute que quelques-uns des architectes et sculpteurs grecs utilisés consciemment dans leurs œuvres. Un exemple serait au moins le Parthénon. Cette circonstance signifiait aussi mathématicien américain Mark Barr, quand il a proposé d'appeler le rapport de deux segments qui forment le nombre d'or, le nombre de lettre j (phi) - la première lettre du nom du grand Phidias, qui dit avoir souvent utilisé le nombre d'or dans ses sculptures. L'une des raisons pour lesquelles les pythagoriciens ont choisi le pentagramme ou étoile à cinq branches, symbole de leurs ordres secrets, est le fait que toute coupe dans la figure est en or à l'égard du plus petit segment adjacent. Beaucoup de mathématiciens, qui vivaient au Moyen Age et de la Renaissance étaient tellement passionnés par l'étude des propriétés extraordinaires de j, il était comme une folie légère.

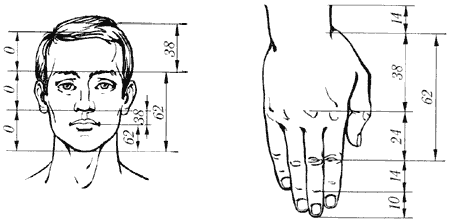
Un exemple est le mot Kepler: "Géométrie a deux trésors: l'un d'entre eux - le théorème de Pythagore, l'autre - la division d'un segment de ligne dans un rapport extrême et moyenne. Le premier peut être appelé une mesure de l'or, la triple est plus comme un bijou. " A la Renaissance, l'attitude exprimée par un nombre j, appelé «divine proportion» ou, après Euclide, "moyenne et extrême."

La «section d'or" terme est entré en usage que dans le dix-neuvième siècle. Beaucoup de propriétés remarquables j, qui se manifeste dans une variété de figures planes et tridimensionnelles ont été recueillies dans le traité Luca Pacioli, publié en 1509 sous le nom «De Divina Proportione» ( «Sur la Divine Proportion») avec des illustrations de Leonardo da Vinci.

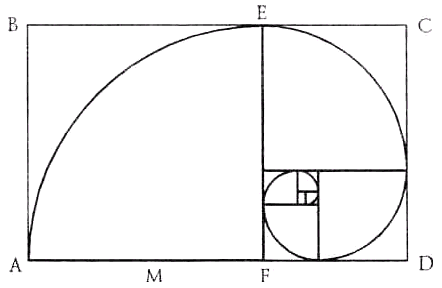
Le nombre j exprime, par exemple, le rapport de la circonférence au rayon de la décagone régulier inscrit. Il y a trois rectangle "d'or" (ie rectangle dont les côtés sont dans le rapport "d'or") de sorte que chaque symétriquement croisé avec deux autres (à angle droit par rapport à chacun d'entre eux), nous pouvons voir que le haut des rectangles "d'or" coïncident avec 12 sommets d'un icosaèdre régulier, et en même temps indiquent la position des centres des faces de 12 dodécaèdre régulier. Rectangle d'or a de nombreuses propriétés inhabituelles. Coupez de la place du rectangle d'or dont le côté est égal au plus petit côté du rectangle, on obtient à nouveau un rectangle d'or plus petit. Continuer à couper des carrés, nous serons plus en plus petits rectangles d'or. Et ils seront placés sur une spirale logarithmique, ce qui est d'une grande importance dans les modèles mathématiques des objets naturels (par exemple, des coquilles d'escargots). pôle spirale se trouve à l'intersection des diagonales du rectangle initial BD et le premier à être coupé AC vertical. En outre, tous les rectangles d'or décroissants diagonales suivantes se trouvent sur ces diagonales.

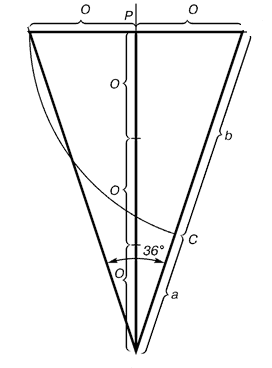
Ceci est un triangle isocèle dans lequel le rapport de la longueur latérale égale à la longueur de 1.618 bases. Le pentagramme chacune des cinq lignes qui composent cette figure, les autres divisions de la section d'or, et les extrémités des étoiles sont des triangles d'or.

En tout temps, les mathématiques, les artistes et les philosophes ont été engagés dans les questions liées à la section d'or. Cependant, la nouvelle «découverte» et est présenté aux scientifiques et aux artistes de la section d'or était au milieu du XIXe siècle. En 1855, un chercheur allemand de la section d'or professeur Zeising publié ses «études esthétiques». Il absolutisée proportion de la section d'or, déclarant universelle pour tous les phénomènes de la nature et de l'art. Dans ses volumineux (457 pages) travaillent Adolf Zeising prouve que toutes les proportions de la section d'or donne le plus grand effet artistique et offre le plus grand plaisir dans la perception. Il absolutisée proportion de la section d'or, déclarant universelle pour tous les phénomènes de la nature et de l'art. Il est dans la section d'or, sur Zeising, se trouve la clé pour comprendre l'ensemble de la morphologie (y compris la structure du corps humain), l'art, l'architecture, et même de la musique. Un autre physiologiste scientifique allemand Gustav Fechner a tenté de justifier ressemble presque Zeising. Pour ce faire, il a mesuré la relation entre les parties en milliers de fenêtres, cadres, cartes à jouer, livres et autres objets rectangulaires, fait en sorte en quoi croisillons tombe croix dans les cimetières divisés base verticale, et a constaté que dans la plupart des cas, il a reçu le nombre légèrement différent de j. Fechner a développé un certain nombre de tests ingénieux, dans lequel on a demandé des expériences de choisir "chère à son cœur" rectangle à partir d'un grand ensemble de rectangles avec différents rapports d'aspect, pour dessiner le polygone le plus «agréable», choisir un coup de pied, etc. Et les expériences ici menées à plusieurs reprises ont montré que les sujets préfèrent une relation semblable à j.

Pour plus d' informations sur l'histoire de la section d' or peut être trouvé à l' adresse http: //bullbear.msm/ru/rus/fr_main513.shtml article intéressant Theodore Landsheydta "fonction Remote de la section d' or", publié dans le Journal de la Société internationale pour la recherche astrologiques (ISAR) «KOSMOS». L'auteur retrace la relation de ces phénomènes disparates tels que les variations dans l'axe solaire, le pourcentage de la surface touchée par la sécheresse, la nourriture l'activité des termites, l'intensité de l'action des médicaments anesthésiques, l'indice de l'activité militaire, la probabilité de la naissance des garçons - et toutes les fluctuations des quantités sont dans la section d'or. Dr Theodore Landsheydt est le directeur de l'Institut des cycles d'activité solaire de la recherche au Canada. L'expert de renommée mondiale sur les relations Soleil-Terre, il a reçu le prix de l'Institut des cycles de Californie en reconnaissance de réalisations exceptionnelles dans ce domaine de la recherche. Il est particulièrement remarquable qu'il ne passe pas, et des fragments d'images fractales de l'ensemble de Mandelbrot, reliant ce qu'il a vu là une spirale logarithmique lois chaotiques fractale de l'univers. Lire l'article peut être inhabituelle sur http://astrologic.ru/library/golden.shtml

Qui veut être malaxée dans les enquêtes philosophiques peuvent aller sur http://www.radiant.ru/~kbb/Page_Gold_midl.shtml pour l'article «La justification philosophique du concept de Golden Section", cependant, à notre avis, pas particulièrement profonde.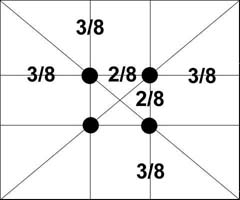

Un exemple intéressant de l'utilisation de la section d' or pour la photo harmonieuse montré sur la page consacrée à l' art photographique www.photoline.ru/tcomp1.shtml Il est basé sur indiqué par des psychologues et des règles de l' art - l'emplacement des principaux composants du châssis au niveau des points singuliers - centres visuels. Tous les quatre de ces points, et ils se trouvent à une distance de 3/8 et 5/8 des bords respectifs de l'avion. L'homme a toujours se concentre sur ces points, quel que soit le format ou le cadre photo.

Ce qui est égal à j? Rappelons la définition: une grande partie se réfère à tout à la majorité. Si plus petit segment de prise comme unité, alors nous pouvons écrire le rapport: (X + 1) / X = X / 1, qui est réduit à une équation quadratique X2-X-1 ordinaire = 0, ce qui est la racine positive. Ce nombre exprime la longueur du segment à la fois X et la valeur de j. Son expansion décimale est 1,61803398 ... Si vous prenez plus par intervalle unité, la longueur de X sera exprimée par l'inverse de la j, alors il y a 1 / j. Curieusement, le 1 / j = 0,61803398 ... Nombre j - le seul nombre positif qui va dans le sens opposé de lui dans l'unité de soustraction. En outre, ce nombre est étroitement liée à certaines propriétés métriques de polygones réguliers et les polyèdres - pentagone, décagone, dodécaèdre, icosaèdre, - comme elle encore 2cos (p / 5). Comme le nombre p, j peut être représenté sous la forme d'une somme d'une série infinie de plusieurs façons. facilité maximale des deux exemples suivants souligne encore une fois la nature fondamentale de j: j j = j nombre irrationnel, ne peut pas être représenté comme une fraction simple. Cependant, si nous utilisons la première de ces formules, interrompant notre tir à la première, deuxième, troisième, etc. signe plus, nous obtenons une série de fractions, progressivement, le haut, le bas j approche: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, ... Les vrais amateurs de mathématiques certainement remarqué, que le dénominateur former une séquence de numéros appelés nombres de Fibonacci. Chacun de ces numéros, à partir de la seconde, est la somme des deux précédents. Au numérateur, sont aussi les nombres de Fibonacci "précédent". Voici l'un des programmes d'options qui calcule la valeur de j pour le premier algorithme, en ajoutant des fractions décroissantes:

Dim Q As Double

Private Sub Form_Load ()

Ouvrir "c: \ qeqq.dat" Pour la sortie Comme 1

Q = 1>

Pour i = 1 à 24

Q = 1 + 1 / Q

Imprimer # 1, i, Q

i Suivant

End Sub

Le programme est écrit en Visual Basic, mais le même algorithme peut être implémenté en Pascal, FORTRAN, BASIC, FoxPro - sur toutes les langues disponibles. Notez que la variable Q est déclarée comme un double, ce double précision. Le point de l'algorithme entier est exprimé dans la déclaration «Q = 1 + 1 / Q» qui est calculé autant de fois que le numéro de série de la fraction est calculée, tout le reste est encadrée. Est-il pas élégant? Le programme de travail sera une table:

1 2 2 1,5
3 1,66666666666667
4 1,6
5 1625
6 1,61538461538462
7 1,61904761904762
8 1,61764705882353
9 1,61818181818182
10 1,61797752808989
11 1,61805555555556
12 1,61802575107296
13 1,61803713527851
14 1,61803278688525
15 1,61803444782168
16 1,61803381340013
17 1,61803405572755
18 1,61803396316671
19 1,6180339985218
20 1,61803398501736
21 1,6180339901756
22 1,61803398820532
23 1,6180339889579
24 1,61803398867044

qui montre comment notre algorithme, se rétrécissant progressivement au nombre j sélectionné. De même, on peut «choisi» au numéro j et en utilisant la seconde formule, les racines carrées:
Dim Q As Double
Private Sub Form_Load ()
Ouvrir "c: \ qeqq.dat" Pour la sortie Comme 1
Q = 1
Pour i = 1 à 24
Q = Sqr (1 + Q)
Imprimer # 1, i, Q
i Suivant
End Sub
Le résultat du programme:

1 1,4142135623731
2 1,55377397403004
3 1,59805318247862
4 1,61184775412525
5 1,61612120650812
6 1,61744279852739
7 1,61785129060967
8 1,61797753093474
9 1,61801654223149
10 1,61802859747023
11 1,618032322752
12 1,61803347392815
13 1,61803382966122
14 1,61803393958879
15 1,61803397355828
16 1,61803398405543
17 1,61803398729922
18 1,61803398830161
19 1,61803398861137
20 1,61803398870709
21 1,61803398873667
22 1,61803398874581
23 1,61803398874863
24 1,6180339887495

La comparaison des résultats parle en faveur de la deuxième méthode, la méthode de la valeur des racines carrées 1,618033 atteint la douzième étape, et la méthode de sommation de seulement seizième fractions. Puisque nous sommes si sérieusement pris le calcul, il serait injuste de simplement ignorer l'interprétation du rapport d'or comme le rapport de deux mandats successifs de la série de Fibonacci. Surtout parce que le sujet lui-même calculer Fibonacci extrêmement intéressant, car il est associé à la notion de récursivité. Quelle est la fonction dans tous les langages de programmation sont (très brièvement - cela fait partie du programme appelé à l'élaboration d'un paramètre variable). Et si la fonction elle-même appelle, une telle technique est appelée récursivité. Dans tous les manuels sur la récursivité de programmation est expliqué par l'exemple de calcul des nombres de Fibonacci, et tous les articles populaires sur ces chiffres vont certainement mentionner récursivité. Sans entrer dans la jungle théorique seulement dire que la récursivité vous permet d'écrire compact en termes de volume du code source du programme. Mais en termes d'utilisation optimale de la récursivité du programme est très douteux. Prenons l'exemple suivant (maintenant sur Turbo Pascal'e), calcule le nous désiré le nombre d'or en utilisant la récursivité. Toute détermination de mise en évidence dans les fonctions FIB pour la première et la deuxième valeur de paramètre est égal à un, et pour chaque successifs délivre en sortie la somme des deux dernières valeurs et les détermine, en se faisant!

programme m; utilise crt;
VAR I: Integer; C: CHAR; F: TEXTE;
FONCTION FIB (T: ENTIER): ENTIER;
commencer
IF (T = 1) OU (T = 2) ALORS
Fib: = 1
AUTRE Fib: = FIB (T-1) + FIB (T-2)
mettre fin;
BEGIN
ASSIGN (F, 'C: \ QQQ.DAT');
REWRITE (F);
clrscr;
POUR I: = 1 A 24 NE COMMENCE
WRITELN (F, I, '', FIB (I), '', FIB (i + 1), '', FIB (I + 1) / FIB (I));
END;
CLOSE (F);
C: = ReadKey;
FIN.

Compte tenu des résultats du programme, nous voyons, comme le rapport entre les deux nombres de Fibonacci adjacents progressivement, le haut, le bas, à proximité de la section d'or.

1 1 1 + 00 1.0000000000E
2 1 2 + 00 2.0000000000E
3 2 3 00 + 1.5000000000E
4 3 5 1.6666666667E + 00
5 5 8 1.6000000000E + 00
6 8 13 00 1.6250000000E +
13 Juillet 21 1.6153846154E + 00
21 Août 34 1.6190476190E + 00
9 34 55 00 1.6176470588E +
10 55 89 00 1.6181818182E +
11 89 144 00 1.6179775281E +
+ 00 12144233 1.6180555556E
+ 00 13233377 1.6180257511E
+ 00 14377610 1.6180371353E
+ 00 15610987 1.6180327869E
16 987 1597 1.6180344478E + 00
17 1597 2584 1.6180338134E + 00
18 2584 4181 + 00 1.6180340557E
19 4181 6765 + 00 1.6180339632E
20 6765 10946 00 + 1.6180339985E
21 10946 17711 1.6180339850E + 00
22 17711 28657 1.6180339902E + 00
23 28657 46368 1.6180339882E + 00
24 46368 75025 1.6180339890E + 00

La valeur de 1.618033 seulement apparu sur 17 étape que la première façon «plus faible», mais, d'autre part, nous avons les valeurs des 24 membres de la série de Fibonacci, et a rencontré récursivité. Mais le programme ne fonctionne pas de façon optimale - Vingtième la valeur considérée pendant environ cinq secondes (pIII-700, et le quarantième d'une minute). Trop de «mouvements» ne une fonction récursive, leur nombre est en croissance comme une augmentation d'avalanche dans le nombre, l'élégance du codage est allé au détriment de la performance. Mais ce que nous avions à faire un programme pour travailler efficacement? Demandez un tableau et le remplir avec la même fonction, mais sans récursion, se référant au nombre de membres ont déjà compté, placé dans le tableau. Le programme fonctionne "immédiatement", mais il ne sera pas si agréable.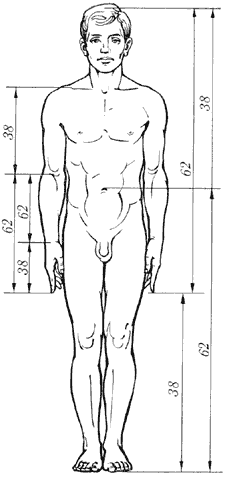

Actuellement Fibonacci intensivement étudié les hommes d'affaires et les économistes. On remarque que les vagues qui décrivent les fluctuations des prix des valeurs mobilières sont des enveloppes de petites vagues, ils, à son tour, encore plus petit, et le nombre de fluctuations à petite échelle dans la période correspond à un plus grand nombre de Fibonacci. Ce fut d'abord suggéré Elliott. Helson Ralph Elliott était un ingénieur. Après une grave maladie au début des années 1930. il a pris l'analyse des prix des actions, en particulier le Dow Jones. Après une série de prédictions très réussie Elliott a publié en 1939 une série d'articles dans le Journal of World Magazine Financial. Ils ont d'abord présenté son point de vue, que le mouvement de l'indice Dow Jones sont soumis à certains rythmes. Selon Elliott, tous ces mouvements suivent la même loi que les marées - la marée devrait refluer, l'action (action) doit contrer (réaction). Ce régime ne dépend pas du temps depuis la structure du marché, pris dans son ensemble, il reste inchangé. Il a écrit: "Lyuboy activité humaine inhérente aux trois traits distinctifs: la forme, le temps et l'attitude - qui sont soumis à la sommation de la suite de Fibonacci." Si vous obtenez une poignée sur les nombres d'onde de Fibonacci et Elliott, vous pouvez devenir riche en jouant sur la bourse. Les parties intéressées peuvent consulter le site Web de Elliott Wave International Internet http://www.elliottwave.com/ Si le mauvais avec les Anglais, et je veux devenir riche - puis passez à http://user.cityline.ru/~esfinkro/index.shtml , il y a une description de l'article sur le Elliot Wave.

L'intérêt pour la section d'or est rafales chauffées et périodiques de la popularité des pyramides. Par exemple, www.rcom.ru/tvv/Dm/str6.shtml peut être trouvé, entre autres signes de la pyramide de Kheops, et contenue dans ses proportions de la section d' or. Ne pas faire sans drôles de choses. Dans la page déjà mentionné http: //bullbear.msm/ru/rus/fr_main513.shtml trouver: "La longueur des faces de la pyramide de Gizeh est 783,3 pieds (238,7 m), la hauteur de la pyramide - 484,4 pieds (147,6 m). La longueur de la face divisée par la hauteur, conduit à la relation P = 1,618. La hauteur de 484,4 pieds correspond à 5813 pouces (08/05/13) - est le nombre de la suite de Fibonacci, "Tout l'humour dans le fait que les anciens Egyptiens ont été mesurés presque rien en pouces. (Mètres ici - est une autre affaire j), et l'apparition des chiffres ici Fibonacci expliqué sans mysticisme nullement impossible. Piramidostroeniem intéressé par les phénomènes modernes et inhabituels qui se produisent dans les pyramides, je vous recommande l'article Pyramids amateur Alexander Golod "Pyramides dans les proportions de la section d' or - la vie du générateur" situé sur http://www.slavaiv.narod.ru/ . La plus grande pyramide de hauteur de 44 mètres a été construit à la fin de 1999, non loin de Moscou, à 38 km de la route de Moscou à Riga, il est non seulement à la télévision, a parlé des miracles qui s'y déroulent. Vous ne pouvez pas dire que les proportions de la pyramide sont soumis a discuté de nos relations. Eh bien, voilà tout. Maintenant, vous non seulement de sélectionner intuitivement le rapport d'aspect du palais est construit par vous, mais vérifier eux, ce qui porte à la section d'or. défi. Martin Gardner, chroniqueur mathématiques amusantes dans la revue Scientific American, a reçu une lettre de ses lecteurs l'information que le ratio moyen de croissance humaine à une hauteur égale au nombril j. Il serait nécessaire de vérifier cela, et les femmes peuvent être mesurées en hauts talons. Et pour les amateurs les plus les plus raffinés - comment changer les résultats des trois programmes suivants, si les calculs ne sont pas en commençant par un, et, par exemple, avec une centaine?

Version imprimable
PS matériau est protégé.
Date de publication 07.03.2004gg

NOUVEAUX ARTICLES ET PUBLICATIONS
	La technologie de fabrication de joints universels pour besvarochnogo, threadless, besflyantsevogo segments de tuyau de raccordement dans les conduites à haute pression (une vidéo)
	technologie de pétrole et de produits pétroliers purification
	Sur la possibilité de déplacer le système mécanique due à des forces internes
	Glow liquide dans un kanaloh diélectrique mince
	La relation entre quantique et classique mécanique
	Les ondes millimétriques en médecine. Un nouveau regard. thérapie IIM
	moteur magnétique
	La source de chaleur sur la base d'unités nososnyh