principal
 D' autres disciplines D' autres disciplines
 livres livres
 Matiquement programuvannya mathématique - Nakonechny S.І. Matiquement programuvannya mathématique - Nakonechny S.І.
|
Matiquement programuvannya mathématique - Nakonechny S.І.
8.8.2. tâches Méthode de rozv'yazuvannya de programuvannya quadratique
Zaznachimo scho vіdomim s teorії analіzu funktsіy Je TAKE tverdzhennya: vіd'єmno signifié forme quadratique Je ugnutoyu et dodatno signifié - opukloyu.
Rozglyanemo vipadok vіd'єmno oznachenoї kvadratichnoї forme, scho pour entrer dans tsіlovu funktsіyu zadachі quadratique programuvannya.
max 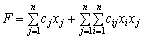 (8,42)
(8,42)
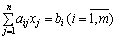 ; (8,43)
; (8,43)
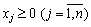 . (8,44)
. (8,44)
Oskіlki tsіlova funktsіya zadachі Je opukloyu et obmezhennya - lіnіynі, tobto viznachayut opuklu mnozhinu rozv'yazkіv recevabilité, la tâche tsya de nalezhit à la tâche opuklogo programuvannya pour yakih spravdzhuєtsya tverdzhennya, scho si Yaky maxima locaux global Yea i. Otzhe, esprit vikoristovuyuchi théorème de Kuhn - Tucker zadachі (8,42) - (8,44) otrimaєmo neobhіdnі que dostatnі esprit optimalnostі plan viglyadі takoї théorème.
Théorème 8.6. Le vecteur X * Je optimale rozv'yazkom zadachі quadratique programuvannya todі, i tіlki todі, si іsnuyut takі m vecteurs de -vimіrnі 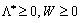 i vecteur n -vimіrny
i vecteur n -vimіrny 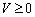 Scho vikonuyutsya esprits:
Scho vikonuyutsya esprits:
(I) 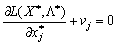 .
. 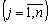 ; (8,45)
; (8,45)
(II) 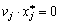 .
. 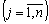 ; (8,46)
; (8,46)
(III) 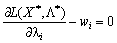 .
. 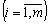 ; (8,47)
; (8,47)
(IV) 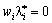 .
. 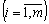 . (8,48)
. (8,48)
INTRODUIT. Zapishemo Lagrange funktsіyu pour programuvannya quadratique zadachі (8,42) - (8,44):
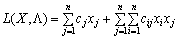 +
+ 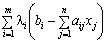 . (8,49)
. (8,49)
Nekhay 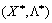 - Sіdlova funktsії point de tobto yak viznachaє programuvannya quadratique plan optimal zadachі Lagrange. Zastosuєmo Théorème 8.4 à virazu (8,49). Pour le théorème du point de habitants
- Sіdlova funktsії point de tobto yak viznachaє programuvannya quadratique plan optimal zadachі Lagrange. Zastosuєmo Théorème 8.4 à virazu (8,49). Pour le théorème du point de habitants 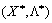 viznachala plan optimal, neobhіdno i dostatno vikonannya drain (8,38) - (8,41):
viznachala plan optimal, neobhіdno i dostatno vikonannya drain (8,38) - (8,41):
pour 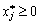 Got vikonuvatis Umov:
Got vikonuvatis Umov:
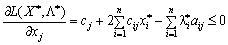 .
. 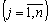 (8,50)
(8,50)
et takozh 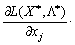
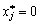 (8,51)
(8,51)
et 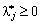 Got vikonuvatis Umov:
Got vikonuvatis Umov:
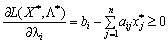 .
. 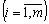 (8,52)
(8,52)
et takozh 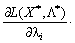
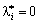 . (8,53)
. (8,53)
Deux vecteurs Vіzmemo 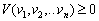 que
que 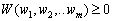 , Le composant sera yakih vvedenі yak dodatkovі zmіnnі en rіvnyannya (8,50) que (8.52). Pour Tsogo viberemo
, Le composant sera yakih vvedenі yak dodatkovі zmіnnі en rіvnyannya (8,50) que (8.52). Pour Tsogo viberemo 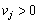 , Yakscho
, Yakscho 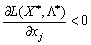 Je
Je 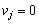 , Yakscho
, Yakscho 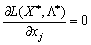 . Analogіchno viberemo
. Analogіchno viberemo 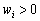 , Yakscho
, Yakscho 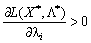 Je
Je 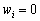 , Yakscho
, Yakscho 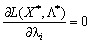 . Les composantes du vecteur de Teper
. Les composantes du vecteur de Teper 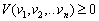 de (8,50) i vіdnіmemo composantes vectorielles
de (8,50) i vіdnіmemo composantes vectorielles 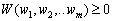 od (8,52). Vrahovuyuchi règles Vibor composante vektorіv, matimemo à (8,50):
od (8,52). Vrahovuyuchi règles Vibor composante vektorіv, matimemo à (8,50):
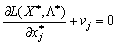 .
. 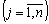 .
.
Zvіdsi: 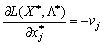 , Que pour (8.51) maєmo:
, Que pour (8.51) maєmo:
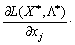
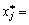
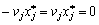 .
.
Analogіchno pour Druha groupies obmezhen:
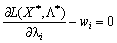 .
. 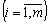 .
.
Zvіdki 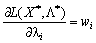 à
à 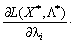
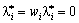 .
.
Théorème apporté.
la théorie d'orientation peut être vikoristati pour pobudovi problèmes méthode efektivnosti de rozv'yazuvannya sur quadratique méthode algorithme simplex programuvannya de osnovі.
Minds (8,45) - (8,49) utvoryuyut stosovno zmіnnih 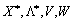 Système (n + m) rіvnyan de 2 (n + m) nevіdomimi.
Système (n + m) rіvnyan de 2 (n + m) nevіdomimi.
Minds (8,47) que (8.48) oznachayut scho zmіnnі 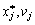 pas mozhut la valeur de odnochasno mère tobto vhoditi en fonction du temps. composants k vecteur de Yakscho
pas mozhut la valeur de odnochasno mère tobto vhoditi en fonction du temps. composants k vecteur de Yakscho 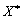 dodatnі puis vіdpovіdnі composants їm du vecteur V i dorіvnyuyut privation zéro (n - k) composant vіdmіnnі od zéro (dodatnі). Otzhe encore
dodatnі puis vіdpovіdnі composants їm du vecteur V i dorіvnyuyut privation zéro (n - k) composant vіdmіnnі od zéro (dodatnі). Otzhe encore 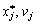 Mère ne sera pas bіlsh nіzh n dodatnih composant. W analogіchnih mіrkuvan schodo rіvnostі (8,48) viplivaє s une fois scho
Mère ne sera pas bіlsh nіzh n dodatnih composant. W analogіchnih mіrkuvan schodo rіvnostі (8,48) viplivaє s une fois scho 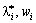 composante bude n + m od vіdmіnnih zéro tobto Tse Mauger Buti les basale scho système de rozv'yazok Minds utvorena (8,45) que (8.47). Pour cette znahodzhennya rozv'yazku mozhna zastosuvati méthode simplex.
composante bude n + m od vіdmіnnih zéro tobto Tse Mauger Buti les basale scho système de rozv'yazok Minds utvorena (8,45) que (8.47). Pour cette znahodzhennya rozv'yazku mozhna zastosuvati méthode simplex.
système Yakscho zaznachena rіvnyan Got plan réalisable (vіn bude єdinim), le plan optimal vіdpovіdnoї zadachі quadratique programuvannya takozh іsnuє.
Rozv'yazuєmo système rіvnyan (8.45) i (8.47) de la méthode simplex. Yak vіdomo, spochatku neobhіdno obmezhen amener le système à l'introduction de l'esprit kanonіchnogo potrіbnoї kіlkostі dodatkovih elle en boîte zmіnnih. Pour que le système des formulaires de l'institution qui viznachennya programme de soutien Pochatkova administré shtuchnі zmіnnі 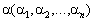 rіvnyannya sous la forme (8.45), sera de base pour le plan de référence SSMSC Perche et zmіnnі
rіvnyannya sous la forme (8.45), sera de base pour le plan de référence SSMSC Perche et zmіnnі 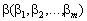 - A grupu rіvnyan (8,47), SSMSC takozh donner bazisnі zmіnnі pour le plan Pochatkova. Potіm pour znahodzhennya base de rozv'yazku le système (8.45) (8.47) rozv'yazuєmo méthode simplex tâche Taku lіnіynogo programuvannya:
- A grupu rіvnyan (8,47), SSMSC takozh donner bazisnі zmіnnі pour le plan Pochatkova. Potіm pour znahodzhennya base de rozv'yazku le système (8.45) (8.47) rozv'yazuєmo méthode simplex tâche Taku lіnіynogo programuvannya:
max 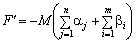 (8,54)
(8,54)
des esprits:
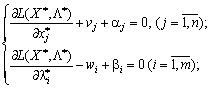 (8,55)
(8,55)
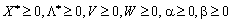 . (8,56)
. (8,56)
Yakscho dans protsesі rozv'yazuvannya zadachі (8,54) - (8,56) OAO Tout shtuchnі zmіnnі sera base vivedenі s 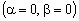 une fois i s valeurs CIM pour zmіnnih znaydenih
une fois i s valeurs CIM pour zmіnnih znaydenih 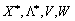 vikonuyutsya Minds (8.46), (8.48), puis znaydeny rozv'yazok quadratique programuvannya de Djé plan optimal (8,42) - (8,44).
vikonuyutsya Minds (8.46), (8.48), puis znaydeny rozv'yazok quadratique programuvannya de Djé plan optimal (8,42) - (8,44).
 problème Rozv'yazati de programuvannya quadratique:
problème Rozv'yazati de programuvannya quadratique:
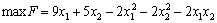
des esprits:
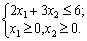
Rozv'yazannya.
Oskіlki tsіlova funktsіya sumoyu lіnіynoї funktsії Virage 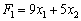 que FORMES kvadratichnoї
que FORMES kvadratichnoї 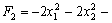
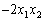 Et le système obmezhen lіnіynoyu Oui, le problème du second degré maєmo programuvannya.
Et le système obmezhen lіnіynoyu Oui, le problème du second degré maєmo programuvannya.
Viznachimo FORMES vue de kvadratichnoї  Pour Chogo vіdshukaєmo korenі la caractéristique rіvnyannya scho vіdpovіdaє matritsі, skladenіy s koefіtsієntіv à zmіnnih danoї funktsії:
Pour Chogo vіdshukaєmo korenі la caractéristique rіvnyannya scho vіdpovіdaє matritsі, skladenіy s koefіtsієntіv à zmіnnih danoї funktsії:
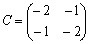 .
.
La rіvnyannyam caractéristique matritsі Avec Bude:
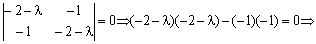
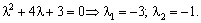
Oskіlki obidva korenі rіvnyannya vіd'єmnі le, alors la forme quadratique caractéristique 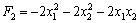 précité et Otzhe, opukloyu de Djé.
précité et Otzhe, opukloyu de Djé.
Zapishemo Lagrange funktsіyu pour tsієї zadachі:
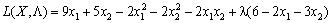 .
.
Skoristaєmosya Théorème 8.4. esprits Neobhіdnі іsnuvannya ekstremumu matimut viglyad:
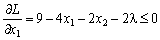 et
et 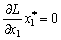 ;
;
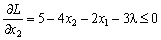 et
et 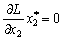 ;
;
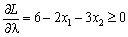 et
et 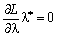 .
.
de 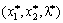 - Coordonnées du point sіdlovoї.
- Coordonnées du point sіdlovoї.
Obmezhennya scho vіdpovіdayut nerіvnostyam, zapishemo en viglyadі:
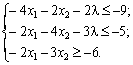
Entrée pour la nerіvnostey Institution de dodatkovі à rіvnyan:
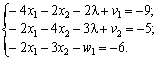
Pour Institution zadachі à kanonіchnoї FORMES pomnozhimo rіvnyannya cutanée (-1):
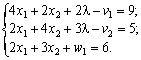
De toute évidence, scho dans danomu razі shtuchnі zmіnnі neobhіdno vvoditi dans Pershi deux rіvnyannya. Un tiers de l'rіvnyannі basale zmіnnoyu Bude 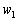 . Maєmo Taku tâche lіnіynogo programuvannya:
. Maєmo Taku tâche lіnіynogo programuvannya:
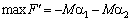 .
.
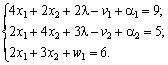
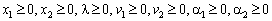 .
.
méthode simplex de Rozv'yazavshi, otrimaєmo:
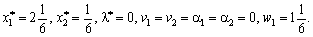
Neobhіdno perevіriti vikonannya esprits:
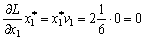 ;
;
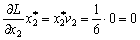 ;
;
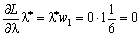 .
.
OAO Tous les esprits vikonuyutsya, Otzhe, 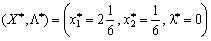 funktsії point de Lagrange de Djé pour programuvannya quadratique zadachі et
funktsії point de Lagrange de Djé pour programuvannya quadratique zadachі et 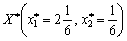 - Optimal zadachі plan pour yakogo valeurs funktsіonala dorіvnyuє:
- Optimal zadachі plan pour yakogo valeurs funktsіonala dorіvnyuє:
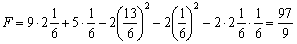 .
.


Commentaires
Commentant, gardez à l' esprit que le contenu et le ton de vos messages peuvent blesser les sentiments des gens réels, montrer du respect et de la tolérance à ses interlocuteurs, même si vous ne partagez pas leur avis, votre comportement en termes de liberté d'expression et de l' anonymat offert par Internet, est en train de changer non seulement virtuel, mais dans le monde réel. Tous les commentaires sont cachés à l'index, le contrôle anti - spam.