principal D' autres disciplines livres Matiquement programuvannya mathématique - Nakonechny S.І.

Matiquement programuvannya mathématique - Nakonechny S.І.

3.4. Butt zastosuvannya teorії dvoїstostі pour znahodzhennya optimale planіv pryamoї que dvoїstoї tâches

problème de conjugaison de dvoh cutanée peut être okremo rozv'yazati contre vstanovlenі théorèmes dvoїstostі zalezhnostі mіzh plan optimal pryamoї que dvoїstoї tâches umozhlivlyuyut znahodzhennya rozv'yazku dvoїstoї zadachі pour nayavnostі régime pryamoї optimal, i navpaki.

Avant zadanoї zadachі lіnіynogo programuvannya zapisati dvoїstu tâche. Rozv'yazati un h eux la méthode simplex est le plan optimal viznachiti Druha zadachі, vikoristovuyuchi spіvvіdnoshennya pershoї dvoїstostі théorème.

max Z = - 5 2 x1 + x2;

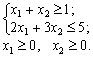
Rozv'yazannya. Perche nіzh zapisati dvoїstu tâche neobhіdno problème direct zvesti à viglyadu standard. Oskіlki tsіlova funktsіya maksimіzuєtsya F i dans sistemі obmezhen Je nerіvnostі puis їh slіd zvesti pour signifier " 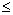». Tom Pershe obmezhennya zadachі pomnozhimo (-1). Pіslya signe Tsogo nerіvnostі zmіnitsya sur protilezhny. Otrimaєmo:

max Z = - 5 2 x1 + x2;

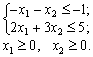
Teper pour le problème de dvoїstu règles de vіdpovіdnimi:

F = min - y1 y2 + 5;

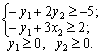
Oskіlki zapisanі zadachі simetrichnі, alors qu'ils peuvent yack s rozv'yazati méthode simplex. Napríklad, viznachimo spochatku pryamoї de façon optimale le plan zadachі. Pour la méthode algorithme simplex de Tsogo.

1. max Z = - 5 2 x1 + x2 + x3 + x4 0 0;

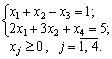
2. Le système d'enregistrement sous forme de vecteur obmezhen Got viglyad:

.

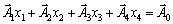de . . . . .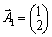

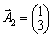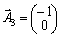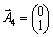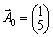Dans vektorіv sistemі pour utvorennya Pochatkova odinichnogo base vіdsutnіy un vecteur. Tom vvedemo zmіnnu boîte à Pershe obmezhennya.

3. Rozshirena tâche lіnіynogo programuvannya bude avec un tel:

max Z = - 5 2 x1 + x2 + x3 + 0 0 x4 - x5 M;

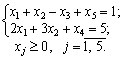
Dans tsіy zadachі x 4 x 5 que - bazisnі zmіnnі et x1, x2, x3 - vіlnі. Nekhay x1 = x2 = x3 = 0, todі x4 = 5; x5 = 1.

Le programme de soutien de Purshia:

X = 0 (0, 0, 0, 5, 1), Z = 0 - M.

4. Loin rozv'yazuvannya pryamoї zadachі déposée en viglyadі simpleksnoї tablitsі:

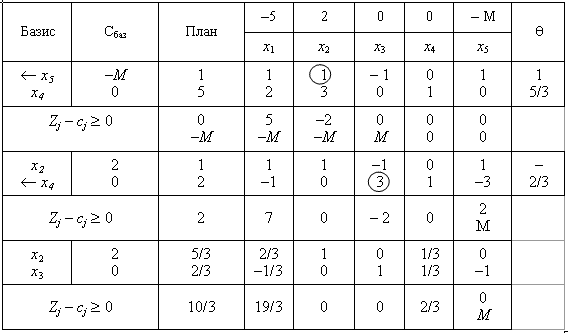
W ostannoї simplex tablitsі zapishemo plan optimal pryamoї zadachі:

X * = (0; 5,3; 2,3; 0), Z max = 10/3.

Le dvoїstostі de Zgіdno Zi pour Perche théorème peut visnovuvati scho plan optimal dvoїstoї zadachі іsnuє i

F min = Z max = 03/10.

Les composantes des vecteurs Y * (dvoїstoї de façon optimale le plan zadachі) viznachimo de la formule:

.

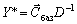de 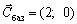que mіstitsya dans stovpchiku "sbaz" ostannoї simplex tablitsі;

.

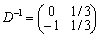Matrice D- 1 takozh mіstitsya dans ostannіy simplex tablitsі dans stovpchikah zmіnnih «x5» que «x4», base SSMSC utvoryuvali Pochatkova.

Otzhe,

.

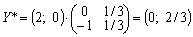min F = - 0 1 x + 5 x 2/3 = 10/3.

Zastosuvavshi pour rozv'yazuvannya pryamoї zadachі méthode simplex, mi znayshli її optimal régime et potіm viznachili optimale rozv'yazok dvoїstoї zadachі for Relief spіvvіdnoshen pershoї dvoїstostі théorème.

Avant zadanoї zadachі lіnіynogo programuvannya zapisati dvoїstu tâche. Rozv'yazavshi dvoїstu tâche grafіchno, plan optimal viznachiti pryamoї zadachі.

min Z = x1 + x2 + x3 2 2;

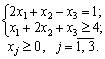
Rozv'yazannya. Pour les règles de vіdpovіdnimi pobuduєmo problème dvoїstu:

max F = y1 + y2 4;

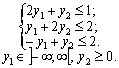
Le nesimetrichnі de Zauvazhimo scho, i Y1 à zmіnna scho Persha vіdpovіdaє rіvnyannyu dans sistemі obmezhen pryamoї zadachі, mère Mauger si Yaky signer et zmіnna v2 - nevіd'єmna privation.

Dvoїsta tâche Got Dvi zmіnnі et Otzhe, її mozhna rozv'yazati grafіchno (Fig. 3.2).

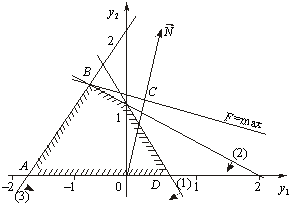
Fig. 3.2

valeurs Naybіlshogo tsіlova funktsіya dvoїstoї zadachі F dosyagaє en tochtsі Dans bagatokutnika ABCD. Її coordonnées viznachimo rozv'yazannyam Sistemi rіvnyan:

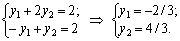
Otzhe, Y * = (- 03/02; 03/04); max F = 1 x (- 2/3) + 4 x 4/3 = 14/3.

Plan Optimal pryamoї zadachі viznachimo for Relief spіvvіdnoshen Druha dvoїstostі théorème.

Pіdstavimo Y * dans le système obmezhen dvoїstoї zadachі i z'yasuєmo, yak vikonuyutsya obmezhennya tsієї zadachі:

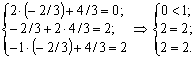
Oskіlki Pershe obmezhennya pour le plan optimal dvoїstoї zadachі vikonuєtsya yak nerіvnіst stricte alors visnovuєmo scho Persha zmіnna pryamoї zadachі dorіvnyuvatime zéro x 1 = 0 (Persha chastina Druha dvoїstostі théorème).

Teper proanalіzuєmo dvoїstoї de façon optimale le plan zadachі. Oskіlki autre composant v2 = 4/3 plan de dodatna, l'autre obmezhennya pryamoї zadachі pour X * vikonuvatimetsya yak strictement rіvnyannya (autre chastina Druha dvoїstostі théorème).

Ob'єdnuyuchi zdobutu іnformatsіyu peut zapisati système obmezhen pryamoї zadachі yak dvoh système rіvnyan dans yakіy x1 = 0, que viznachiti Rasht zmіnnih:

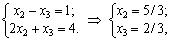
tobto = X * (0; 5/3; 2/3), min Z = 0 + 1 x 2 x 2 x 5/3 + 2/3 = 14/3.

Umov min Z = max F = 14/3 vikonuєtsya, i que X * = (0, 5/3, 2/3); Y * = (- 2/3; 4/3 ) Je optimal régime vіdpovіdno pryamoї que dvoїstoї tâches.

Viznachiti, chi Je takі optimale Plagne sformulovanoї zadachі lіnіynogo programuvannya:

12 min Z = x1 - x2 + x3 2 4;

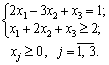
a) X = (8/7, 3/7, 0); b) X = (0; 5,1; 8,5); c) X = (1/3, 0, 1/3).

Rozv'yazannya. problèmes de rozv'yazuvannya Principe de ce type ґruntuєtsya sur le théorème de vikoristannі Druha. Neobhіdno pobuduvati dvoїstu tâche un dopuskayuchi plan de scho vіdpovіdny x ∈ viznachiti de manière optimale de façon optimale rozv'yazok dvoїstoї zadachі. Yakscho à tsomu ekstremalnі valeurs tsіlovih funktsіy sera odnakovimi pour la valeur, puis mijoté correctement. Protilezhne mozhna visnovuvati tels vipadkah:

1. Yakscho zaproponovany le plan X est inacceptable, non tobto zadovolnyaє système obmezhen pryamoї zadachі.

2. Yakscho régime viznacheny de dvoїstoї zadachі inacceptable, tobto pas zadovolnyaє OAO Toutes obmezhennya dvoїstoї zadachі.

3. Yakscho plan de viznacheny dvoїstoї zadachі recevabilité, ale pour les valeurs de ekstremalne Demba tsіlovoї funktsії F ne dorіvnyuє pas funktsії les valeurs Z, tobto pas vikonuєtsya Umov pershoї dvoїstostі théorème.

La tâche Zapishemo de pryamoї à zadachі lіnіynogo programuvannya:

F = max y1 y2 + 2;

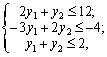
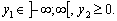
Perevіrimo zaproponovanі Plagne sur optimalnіst.

1. X = (8/7, 3/7, 0). Pіdstavimo Yogo dans obmezhen pryamoї zadachі:

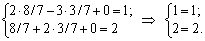
Obidva obmezhennya vikonuyutsya, i à X = (8/7, 3/7, 0) Je plan réalisable pryamoї zadachі. Pripustimo Teper Plan scho zaznacheny Je plan optimal pryamoї zadachі. Todі rozrahuєmo pour la valeur Demba tsіlovoї funktsії: Z = 12 x 8/7-4 3/7 x 2 + x 0 = 12.

Skoristaєmosya autres théorèmes dvoїstostі viznachimo vіdpovіdny dvoїstoї zadachі plan. Oskіlki x1 = 8/7> 0; x2 = 3/7> 0, puis par une autre zgіdno de Chastain Druha Théorème dvoїstostі mozhna zapisati Pershe que d' autres obmezhennya rіvnyannya yack i viznachiti y1 que v2:

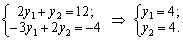
Pіdstavimo valeur tsі dans tretє obmezhennya Sistemi dvoїstoї zadachі:

;

.

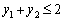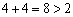Pour les valeurs de viznachenih y1 = 4; v2 = 4 tse obmezhennya pas vikonuєtsya, je prévois de vіdpovіdny y = (4; 4) Je irrecevabilité jusqu'à dvoїstoї zadachі. Vnaslіdok Tsogo nos hypothèses, scho X = (8/7, 3/7, 0) Je plan optimal pryamoї zadachі, viyavilosya pomilkovim.

2. X = (0; 5,1; 5,8). Plan Pіdstavimo Tsey dans le système obmezhen pryamoї zadachі:

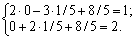
Plan Faisable, i pour Demba Z = 12 x 0 - 4 x 1/5 + 2 x 8/5 = 12/5.

Viznachimo plan de vіdpovіdny dvoїstoї zadachі. composants Oskіlki que x 2 x 3 dodatnі, d' autres i tretє obmezhennya dvoїstoї zadachі mozhna zapisati yak rіvnyannya:

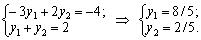
Perevіrimo, chi vikonuєtsya Pershe obmezhennya dvoїstoї zadachі pour les valeurs de viznachenih Y1 v2: 2 x 8/5 + 2/5 = 18/5 <12 Otzhe, Pershe obmezhennya vikonuєtsya, i à v = (8/5, 2/5) je plan réalisable dvoїstoї zadachі. Pour Demba

F = 8/5 + 2 x 2/5 = 12/5 = Z.

W regard autour de vikladene mozhna visnovuvati scho Y * = (8/5; 2/5) Je optimale le plan dvoїstoї zadachі et X * = (0; 1/5; 8/5) - plan optimal pryamoї zadachі.

Notre compotes vіdnosno zaproponovanogo régime viyavilosya correctement.

3. X = (1/3, 0, 1/3). Pour le plan d'Tsogo obmezhennya pryamoї zadachі vikonuyutsya comme suit:

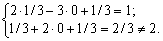
Oskіlki X = (1/3, 0, 1/3) Je irrecevabilité du plan, le vіn pas plan optimal Mauger Buti takozh pryamoї zadachі.

Otzhe, perevіrka zaproponovanih planіv sur optimalnіst a donné takі résultat de: a) ni; b) de telle sorte que X = (0; 1/5; 8/5), min Z = 12/5; c) Ni.