- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
2.2. Загальна економіко-математична модель задачі лінійного програмування
Загальна лінійна економіко-математична модель економічних процесів та явищ — так звана загальна задача лінійного програмування подається у вигляді:
 (2.1)
(2.1)
за умов:
 (2.2)
(2.2)
 (2.3)
(2.3)
Отже, потрібно знайти значення змінних x1, x2, …, xn, які задовольняють умови (2.2) і (2.3), і цільова функція (2.1) набуває екстремального (максимального чи мінімального) значення.
Для довільної задачі математичного програмування у § 1.2 були введені поняття допустимого та оптимального планів.
Для загальної задачі лінійного програмування використовуються такі поняття.
Вектор Х = (х1, х2, …, хn), координати якого задовольняють систему обмежень (2.2) та умови невід’ємності змінних (2.3), називається допустимим розв’язком (планом) задачі лінійного програмування.
Допустимий план Х = (х1, х2, …, хn) називається опорним планом задачі лінійного програмування, якщо він задовольняє не менше, ніж m лінійно незалежних обмежень системи (2.2) у вигляді рівностей, а також обмеження (2.3) щодо невід’ємності змінних.
Опорний план Х = (х1, х2, …, хn), називається невиродженим, якщо він містить точно m додатних змінних, інакше він вироджений.
Опорний план  , за якого цільова функція (2.1) досягає масимального (чи мінімального) значення, називається оптимальним розв’язком (планом) задачі лінійного програмування.
, за якого цільова функція (2.1) досягає масимального (чи мінімального) значення, називається оптимальним розв’язком (планом) задачі лінійного програмування.
Задачу (2.1)—(2.3) можна легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (2.2) всі bi (i = 1, 2, …, m) невід’ємні, а всі обмеження є рівностями.
Якщо якесь bi від’ємне, то, помноживши i-те обмеження на (– 1), дістанемо у правій частині відповідної рівності додатне значення. Коли i-те обмеження має вигляд нерівності аi1х1 + аi2х2 + … + аinxn ≤ bi, то останню завжди можна звести до рівності, увівши додаткову змінну xn + 1: ai1x1 + ai2x2 + … + + ain xn + xn + 1 = bi.
Аналогічно обмеження виду аk1x1 + ak2x2 + … + aknxn ≥ bk зводять до рівності, віднімаючи від лівої частини додаткову змінну хn + 2, тобто: ak1x1 + ak2x2 + … + aknxn – xn + 2 = bk (хn+1 ≥ 0, хn+2 ≥ 0).
Доведемо, що заміна нерівностей рівняннями за допомогою введення додаткових змінних не змінить розв’язку початкової задачі. Розглянемо лінійну нерівність з n невідомими:
 (2.4)
(2.4)
Для зведення нерівності (2.4) до рівняння необхідно до її лівої частини додати деяку невід’ємну величину хn + 1 ≥ 0. У результаті дістаємо лінійне рівняння, яке містить n+1 змінну:
a1x1 + a2x2 + … + anxn + xn + 1 = b. (2.5)
Теорема 2.1. Кожному розв’язку 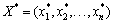 нерівності (2.4) відповідає єдиний розв’язок
нерівності (2.4) відповідає єдиний розв’язок 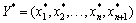 рівняння (2.5), який одночасно є розв’язком нерівності (2.4), і, навпаки, кожному розв’язку
рівняння (2.5), який одночасно є розв’язком нерівності (2.4), і, навпаки, кожному розв’язку 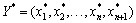 рівняння (2.5) і нерівності (2.4) відповідає єдиний розв’язок
рівняння (2.5) і нерівності (2.4) відповідає єдиний розв’язок  нерівності (2.4).
нерівності (2.4).
Доведення: Нехай X* — розв’язок нерівності (2.4), тоді підстановкою  нерівність виконується:
нерівність виконується:
 .
.
Перенесемо ліву частину даної нерівності в праву і позначимо вираз у правій частині через  , тобто:
, тобто:

Отже, розв’язок  задовольняє рівняння (2.5) і водночас нерівність (2.4). Дійсно, і при підстановці
задовольняє рівняння (2.5) і водночас нерівність (2.4). Дійсно, і при підстановці  в рівняння маємо:
в рівняння маємо: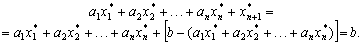
Навпаки, нехай Y* задовольняє рівняння (2.5) і нерівність (2.4), тобто:
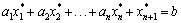 і
і 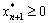 .
.
Тоді, відкидаючи в лівій частині рівності невід’ємну величину  , отримаємо нерівність:
, отримаємо нерівність:
 .
.
Created/Updated: 25.05.2018
 |
|