- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
2.5. Основні властивості розв’язків задачі лінійного програмування
Властивості розв’язків задачі лінійного програмування формулюються у вигляді чотирьох теорем (доведення теорем та їх наслідки наведено нижче).
Властивість 1. (Теорема 2.2) Множина всіх планів задачі лінійного програмування опукла.
Властивість 2. (Теорема 2.3) Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.
Властивість 3. (Теорема 2.4) Якщо відомо, що система векторів A1, A2, …, Ak (k ≤ n) у розкладі A1x1 +A2x2 + … + Anxn = A0, X ≥ 0 лінійно незалежна і така, що
A1x1 + A2x2 + … + Akxk = A0,
де всі xj ≥ 0, то точка X = (x1, x2, …, xk, 0, …, 0) є кутовою точкою багатогранника розв’язків.
Властивість 4. (Теорема 2.5) Якщо X = (x1, x2, …, xn) — кутова точка багатогранника розв’язків, то вектори в розкладі A1x1 + + A2x2 + … + Anxn = A0, X ≥ 0, що відповідають додатним xj, є лінійно незалежними.
Доведемо сформульовані теореми.
Теорема 2.2. Множина всіх планів задачі лінійного програмування опукла.
Доведення. Необхідно довести, що коли X1 та X2 — плани задачі лінійного програмування (2.1)—(2.3), то їх опукла комбінація 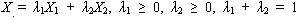
Так як X1 і X2 — плани задачі, то виконуються такі співвідношення:
AX1 = A0, X1 ≥ 0; AX2 = A0, X2 ≥ 0.
Якщо підставити в систему обмежень значення X, то отримаємо:
Отримали, що X задовольняє систему обмежень задачі лінійного програмування (2.2), і оскільки 
Теорема 2.3. Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин багатогранника розв’язків. Якщо цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.
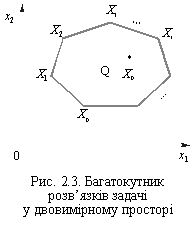
Доведення. Припустимо, що багатогранник розв’язків задачі обмежений і має скінченну кількість кутових точок. Позначимо його через Q. У двовимірному просторі Q має вид багатокутника, що зображено на рис. 2.3. Позначимо кутові точки через Х1, Х2, ..., Хр, а оптимальний план — Х0.
Задача (2.1) — (2.3) розв’язується на максимум, отже, при будь-якому Х із Q для значення Х0 виконується нерівність F(X0) ≥ F(X). Якщо Х0 — кутова точка, то перша частина теореми доведена. Припустимо, що Х0 не є кутовою точкою, тоді Х0 є точкою, яка належить опуклій множині (доведено в попередній теоремі). Отже, її можна подати як опуклу лінійну комбінацію кутових точок множини Q, тобто
X0 = λ1X1 + λ2X2 + … + λpXp,
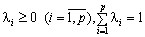 .
.
У зв’язку з тим, що F(X) — лінійна функція, отримаємо:
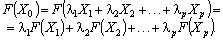 (2.16)
(2.16)
У такому розкладі серед значень F(Xi) 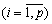 вибираємо найбільше (припустимо, що воно відповідає кутовій точці
вибираємо найбільше (припустимо, що воно відповідає кутовій точці 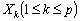 і позначимо його через m, тобто
і позначимо його через m, тобто 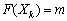 . Замінимо в (2.16) кожне значення F(Xi) цим найбільшим значенням. Оскільки
. Замінимо в (2.16) кожне значення F(Xi) цим найбільшим значенням. Оскільки 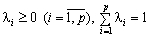 , то
, то
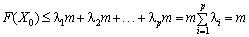 .
.
За припущенням Х0 — оптимальний план, отже, з одного боку, F(X0) ≥ F(Xk) = m, а з другого, доведено, що F(X0) ≤ m, значить, F(X0) = m = F(Xk), де Xk — кутова точка. Отже, лінійна функція досягає максимального значення в кутовій точці (Xk).
Для доведення другої частини теореми припустимо, що F(X) набирає максимальних значень більше, ніж в одній кутовій точці, наприклад у точках Х1, Х2, ..., Хq, (1 ≤ q ≤ p), тоді F(X1) = F(X2) = … = F(Xq) = m. Якщо Х опукла лінійна комбінація цих кутових точок, то:
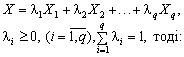
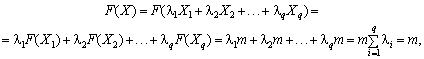
тобто лінійна функція F набирає максимальних значень у довільній точці Х, яка є опуклою лінійною комбінацією кутових точок Х1, Х2, ..., Хq.
Зауваження. Якщо багатокутник розв’язків — необмежена область (рис. 2.4), то не кожну точку можна подати у вигляді опуклої лінійної комбінації її кутових точок. У такому разі задачу лінійного програмування з багатокутником розв’язків, що є необмеженою областю, можна звести до задачі з обмеженою областю, ввівши в систему додаткове обмеження х1 + х2 ≤ L, де L — достатньо велике число. Введення цього обмеження означає відтинання прямою х1 + х2 = L від багатокутної необмеженої області обмеженого багатокутника, для якого виконується наведена теорема.
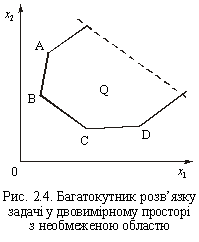
Очевидно, що координати кутових точок, які утворяться в результаті введення нового обмеження, залежать від L. Якщо в одній з них лінійна функція набирає максимального значення, то воно залежить від L. Змінюючи L, значення функціонала можна зробити як завгодно великим, а це означає, що лінійна функція необмежена на багатограннику розв’язків.
Теорема 2.4. Якщо відомо, що система векторів 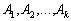 (k ≤ n) у розкладі
(k ≤ n) у розкладі 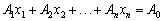 ,
, 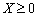 лінійно незалежна і така, що
лінійно незалежна і така, що
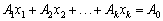 ,
,
де всі xj ≥ 0, то точка X = (x1, x2, …, xk, 0, …, 0) є кутовою точкою багатогранника розв’язків.
Доведення. Припустимо, що точка Х не є кутовою. Тоді вона може бути виражена опуклою лінійною комбінацією двох інших точок Х1 та Х2 багатокутника розв’язків, тобто:
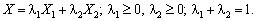
Компоненти векторів Х1 та Х2, значення λ1 і λ2 невід’ємні і останні n – k компонентів вектора Х дорівнюють нулю, тому відповідні n – k компонент векторів Х1 та Х2 також мають дорівнювати нулю, тобто
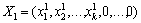 ,
,
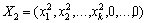 .
.
Оскільки Х1 та Х2 — плани, то
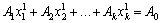 ,
,
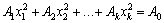 .
.
Віднімаючи від першого рівняння друге, отримаємо:
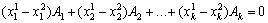 .
.
За припущенням вектори 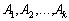 лінійно незалежні, тому останнє співвідношення виконується, якщо
лінійно незалежні, тому останнє співвідношення виконується, якщо
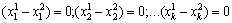 .
.
Звідси: 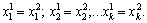
Отже, Х неможливо подати як опуклу лінійну комбінацію двох інших точок багатокутника розв’язків. Значить, Х — кутова точка.
Теорема 2.5. Якщо 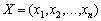 — кутова точка багатогранника розв’язків, то вектори в розкладі
— кутова точка багатогранника розв’язків, то вектори в розкладі 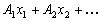
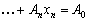 ,
, 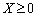 , що відповідають додатним
, що відповідають додатним 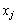 , є лінійно незалежними.
, є лінійно незалежними.
Доведення. Не порушуючи загальності, можна вважати нерівними нулю перші k елементів вектора Х, отже,
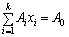 .
.
Здійснимо доведення від супротивного. Припустимо, що система векторів 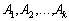 лінійно залежна. Тоді існують такі числа
лінійно залежна. Тоді існують такі числа 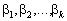 , не всі рівні нулю, за яких виконується співвідношення:
, не всі рівні нулю, за яких виконується співвідношення:
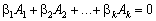 .
.
За умовою
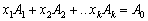 .
.
Задамо деяке число 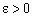 , помножимо на нього першу рівність, далі результат спочатку додамо до другого, а потім віднімемо від другого рівняння:
, помножимо на нього першу рівність, далі результат спочатку додамо до другого, а потім віднімемо від другого рівняння:
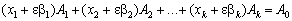 ,
,
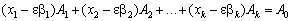 .
.
Отже, система рівнянь задачі лінійного програмування 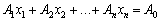 має два розв’язки, які можуть і не бути планами.
має два розв’язки, які можуть і не бути планами.
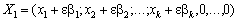
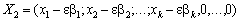 .
.
Всі хі > 0, тому число 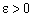 можна вибрати настільки малим, що всі перші компоненти
можна вибрати настільки малим, що всі перші компоненти 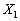 та
та 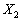 набуватимуть додатних значень, тоді
набуватимуть додатних значень, тоді 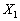 та
та 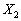 — плани. При цьому
— плани. При цьому 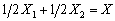 , тобто Х — опукла лінійна комбінація точок Х1 та Х2, що суперечить умові теореми, оскільки Х — кутова точка.
, тобто Х — опукла лінійна комбінація точок Х1 та Х2, що суперечить умові теореми, оскільки Х — кутова точка.
Припущення стосовно лінійної залежності векторів 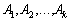 привело до суперечності. Отже, воно є неправильним, а система векторів — лінійно незалежна.
привело до суперечності. Отже, воно є неправильним, а система векторів — лінійно незалежна.
Наслідок 1. Оскільки вектори 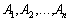 мають розмірність m, то кутова точка багатокутника розв’язків має не більше, ніж m додатних компонентів
мають розмірність m, то кутова точка багатокутника розв’язків має не більше, ніж m додатних компонентів 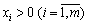 .
.
Наслідок 2. Кожній кутовій точці багатокутника розв’язків відповідає 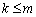 лінійно незалежних векторів системи
лінійно незалежних векторів системи 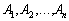 .
.
З наведених властивостей можна висновувати:
якщо функціонал задачі лінійного програмування обмежений на багатограннику розв’язків, то:
- існує така кутова точка багатогранника розв’язків, в якій лінійний функціонал досягає свого оптимального значення;
- кожний опорний план відповідає кутовій точці багатогранника розв’язків.
Тому для розв’язання задачі лінійного програмування необхідно досліджувати лише кутові точки багатогранника (опорні плани), не включаючи до розгляду внутрішні точки множини допустимих планів.
Created/Updated: 25.05.2018
 |
|