- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
2.6. Графічний метод розв’язування задач лінійного програмування
Для розв’язування двовимірних задач лінійного програмування, тобто задач із двома змінними, а також деяких тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування. Обмежене використання графічного методу зумовлене складністю побудови багатогранника розв’язків у тривимірному просторі (для задач з трьома змінними), а графічне зображення задачі з кількістю змінних більше трьох взагалі неможливе.
Розглянемо задачу.
Знайти
 (2.17)
(2.17)
за умов:
 (2.18)
(2.18)
 . (2.19)
. (2.19)
Припустимо, що система (2.18) за умов (2.19) сумісна і багатокутник її розв’язків обмежений.
Згідно з геометричною інтерпретацією задачі лінійного програмування (§ 2.4) кожне і-те обмеження-нерівність у (2.18) визначає півплощину з граничною прямою  (і = 1, 2, …, т). Системою обмежень (2.18) графічно можна зобразити спільну частину, або переріз усіх зазначених півплощин, тобто множину точок, координати яких задовольняють всі обмеження задачі — багатокутник розв’язків.
(і = 1, 2, …, т). Системою обмежень (2.18) графічно можна зобразити спільну частину, або переріз усіх зазначених півплощин, тобто множину точок, координати яких задовольняють всі обмеження задачі — багатокутник розв’язків.
Умова (2.19) невід’ємності змінних означає, що область допустимих розв’язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція задачі лінійного програмування геометрично інтерпретується як сім’я паралельних прямих с1х1 + с2х2 = const.
Скористаємося для графічного розв’язання задачі лінійного програмування властивостями, наведеними в § 2.5:
якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатокутника розв’язків. Якщо ж цільова функція досягає екстремального значення більш як в одній вершині багатокутника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин.
Отже, розв’язати задачу лінійного програмування графічно означає знайти таку вершину багатокутника розв’язків, у результаті підстановки координат якої в (2.17) лінійна цільова функція набуває найбільшого (найменшого) значення.
Алгоритм графічного методу розв’язування задачі лінійного програмування складається з таких кроків:
1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях задачі (2.18) знаків нерівностей на знаки рівностей.
2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.
3. Знаходимо багатокутник розв’язків задачі лінійного програмування.
4. Будуємо вектор  , що задає напрям зростання значення цільової функції задачі.
, що задає напрям зростання значення цільової функції задачі.
5. Будуємо пряму с1х1 + с2х2 = const, перпендикулярну до вектора  .
.
6. Рухаючи пряму с1х1 + с2х2 = const в напрямку вектора  (для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального зна- чення.
(для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального зна- чення.
7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.
У разі застосування графічного методу для розв’язування задач лінійного програмування можливі такі випадки:
1. Цільова функція набирає максимального значення в єдиній вершині А багатокутника розв’язків (рис. 2.5).
2. Максимального значення цільова функція досягає в будь-якій точці відрізка АВ (рис. 2.6). Тоді задача лінійного програмування має альтернативні оптимальні плани.
3. Задача лінійного програмування не має оптимальних планів: якщо цільова функція необмежена згори (рис. 2.7) або система обмежень задачі несумісна (рис. 2.8).

Рис. 2.5 Рис. 2.6

Рис. 2.7 Рис. 2.8
4. Задача лінійного програмування має оптимальний план за необмеженої області допустимих розв’язків (рис. 2.9 і 2.10). На рис. 2.9 у точці В маємо максимум, на рис. 2.10 у точці А — мінімум, на рис. 2.11 зображено, як у разі необмеженої області допустимих планів цільова функція може набирати максимального чи мінімального значення у будь-якій точці променя.

Рис. 2.9 Рис. 2.10
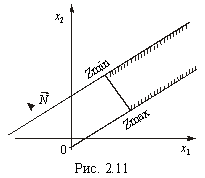
Розв’язувати графічним методом можна також задачі лінійного програмування n-вимірного простору, де  , якщо при зведенні системи нерівностей задачі до системи рівнянь шляхом введення додаткових змінних кількість змінних n на дві більша, ніж число обмежень m, тобто
, якщо при зведенні системи нерівностей задачі до системи рівнянь шляхом введення додаткових змінних кількість змінних n на дві більша, ніж число обмежень m, тобто 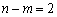 .
.
Тоді, як відомо з курсу вищої математики, можна дві з n змінних, наприклад х1 та х2, вибрати як вільні, а інші m зробити базисними і виразити через вільні. Припустимо, що це зроблено. Отримаємо 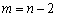 рівнянь вигляду:
рівнянь вигляду:

Оскільки всі значення  , то мають виконуватись умови:
, то мають виконуватись умови:
 ,
,
 (2.19.1)
(2.19.1)
Розглянемо, як можна зобразити ці умови геометрично. Візьмемо, наприклад, першу з них:

Узявши величину х3 рівною своєму крайньому значенню — нулю, отримаємо рівняння:
 .
.
Це рівняння прямої. Для такої прямої  , по одну сторону від неї
, по одну сторону від неї  , а по другу —
, а по другу —  . Відмітимо ту сторону прямої
. Відмітимо ту сторону прямої  , де
, де  .
.
В аналогічний спосіб побудуємо і всі інші обмежуючі прямі:  ;
;  ;...;
;...; і відмітимо для кожної з них півплощину, де відповідна змінна більше нуля.
і відмітимо для кожної з них півплощину, де відповідна змінна більше нуля.
У такий спосіб отримують n – 2 прямі та дві осі координат (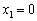 ,
, ). Кожна з них визначає півплощину, де виконується умова
). Кожна з них визначає півплощину, де виконується умова 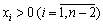 . Частина площини в
. Частина площини в  належить водночас всім півплощинам, утворюючи багатокутник допустимих розв’язків.
належить водночас всім півплощинам, утворюючи багатокутник допустимих розв’язків.
Припустимо, що в задачі необхідно знайти максимальне значення функціонала:
 .
.
Підставивши вирази для 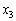 ,
,  ,
, 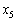 , ...;
, ...; з (2.19.1) у цей функціонал, зведемо подібні доданки і отримаємо вираз лінійної функції F всіх n змінних лише через дві вільні змінні
з (2.19.1) у цей функціонал, зведемо подібні доданки і отримаємо вираз лінійної функції F всіх n змінних лише через дві вільні змінні  та
та  :
:
 ,
,
де 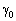 — вільний член, якого в початковому вигляді функціонала не було.
— вільний член, якого в початковому вигляді функціонала не було.
Очевидно, що лінійна функція  досягає свого максимального значення за тих самих значень
досягає свого максимального значення за тих самих значень  та
та  , що й
, що й  . Отже, процедура відшукання оптимального плану з множини допустимих далі здійснюється за алгоритмом для випадку двох змінних.
. Отже, процедура відшукання оптимального плану з множини допустимих далі здійснюється за алгоритмом для випадку двох змінних.
 Розв’язати графічним методом задачу лінійного програмування
Розв’язати графічним методом задачу лінійного програмування


 .
.
Розв’язання. Маємо n = 7 — кількість змінних, m = 5 — кількість обмежень. Виберемо як вільні змінні х1 та х2 і виразимо через них всі інші базисні змінні. З першого рівняння маємо:  (2.19.2)
(2.19.2)
З третього рівняння:
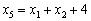 , (2.19.3)
, (2.19.3)
а з четвертого:
 . (2.19.4)
. (2.19.4)
Підставляючи (2.19.2) в друге рівняння системи і (2.19.4) в останнє, розв’язуємо їх відносно х4 та х7. Отримаємо:
 ;
;
 .
.
Далі за алгоритмом беремо х1 = 0 та х2 = 0 — координатні осі; інші обмежуючі прямі знаходимо, узявши х3 = 0, х4 = 0, х5 = 0, х6 = 0, х7 = 0. Багатокутник допустимих розв’язків зображено на рис. 2.12.

Рис. 2.12
Знайдемо вигляд функціонала, вираженого через х1 та х2. Для цього знайдені щойно вирази для х3, х4, х5, х6 та х7 через вільні змінні х1 і х2 підставимо у функціонал і, звівши подібні члени, отримаємо: 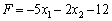 . Відкидаючи вільний член, маємо:
. Відкидаючи вільний член, маємо: 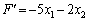 . Будуємо вектор
. Будуємо вектор  (–5, –2), перпендикулярно до нього — пряму F'. Рухаючи пряму F' в напрямку, протилежному
(–5, –2), перпендикулярно до нього — пряму F'. Рухаючи пряму F' в напрямку, протилежному  (необхідно знайти мінімальне значення функції F), отримаємо точку мінімуму — А (рис. 2.13).
(необхідно знайти мінімальне значення функції F), отримаємо точку мінімуму — А (рис. 2.13).

Рис. 2.13
У точці А перетинаються дві обмежуючі прямі: х6 = 0 та х7 = 0. Отже, для відшукання її координат необхідно розв’язати систему рівнянь:

Розв’язком системи є 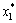 = 8,5;
= 8,5;  = 5. Підставивши ці значення у відповідні вирази, знайдемо оптимальні значення базисних змінних:
= 5. Підставивши ці значення у відповідні вирази, знайдемо оптимальні значення базисних змінних:
 = 0,5;
= 0,5;  = 16,5;
= 16,5; 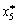 = 17,5;
= 17,5; 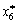 = 0;
= 0;  = 0.
= 0.
Підстановкою значень  та
та 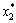 в лінійну функцію F отримуємо значення цільової функції:
в лінійну функцію F отримуємо значення цільової функції:
 .
.
2.7. Приклади розв’язування задач графічним методом
Розглянемо застосування графічного методу для розв’язування деяких економічних задач.
 Фірма спеціалізується на виробництві офісних меблів, зокрема вона випускає два види збірних книжкових полиць — А та В. Полиці обох видів виготовляють на верстатах 1 та 2. Тривалість обробки деталей однієї полиці кожної моделі подано в табл. (2.4).
Фірма спеціалізується на виробництві офісних меблів, зокрема вона випускає два види збірних книжкових полиць — А та В. Полиці обох видів виготовляють на верстатах 1 та 2. Тривалість обробки деталей однієї полиці кожної моделі подано в табл. (2.4).
Таблиця 2.4
ТРИВАЛІСТЬ ВИГОТОВЛЕННЯ КНИЖКОВИХ ПОЛИЦЬ
Верстат |
Тривалість обробки полиці моделі, хв. |
Ресурс робочого часу верстатів, год. на тиждень |
|
А |
В |
||
1 |
30 |
15 |
40 |
2 |
12 |
26 |
36 |
Прибуток фірми від реалізації однієї полиці моделі А дорівнює 50 у. о., а моделі В — 30 у. о. Вивчення ринку збуту показало, що тижневий попит на книжкові полиці моделі А ніколи не перевищує попиту на модель В більш як на 30 одиниць, а продаж полиць моделі В не перевищує 80 одиниць на тиждень.
Необхідно визначити обсяги виробництва книжкових полиць цих двох моделей, що максимізують прибуток фірми. Для цього слід побудувати економіко-математичну модель поставленої задачі та розв’язати її графічно.
Побудова математичної моделі. Змінними в моделі є тижневі обсяги виробництва книжкових полиць моделей А та В. Нехай х1 — кількість полиць моделі А, виготовлених фірмою за тиждень, а х2 — кількість полиць моделі В. Цільова функція задачі — максимум прибутку фірми від реалізації продукції. Математично вона подається так:
 .
.
Обмеження задачі враховують тривалість роботи верстатів 1 та 2 для виготовлення продукції та попит на полиці різних моделей.
Обмеження на тривалість роботи верстатів 1 та 2 мають вид:
для верстата 1:
30х1 + 15х2 ≤ 2400 (хв);
для верстата 2:
12х1 + 26х2 ≤ 2160 (хв).
Обмеження на попит записуються так:
х1 – х2 ≤ 30 та х2 ≤ 80.
Загалом економіко-математичну модель цієї задачі можна записати так:
max Z = 50Х1 + 30Х2 (2.20)
за умов:
 
|
|
Ця економіко-математична модель є моделлю задачі лінійного програмування, що містить лише дві змінні, і тому може бути розв’язана графічно.
Розв’язання. Перший крок згідно з графічним методом полягає в геометричному зображенні допустимих планів задачі, тобто у визначенні такої області, де водночас виконуються всі обмеження моделі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис. 2.14). Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї з півплощин задовольняють розглядувану нерівність, а іншої — ні. Щоб визначити необхідну півплощину (на рис. 2.14 її напрям позначено стрілкою), потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. Інакше таким зображенням є інша півплощина.

Рис. 2.14
Умова невід’ємності змінних х1 ≥ 0, х2 ≥ 0 обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі — шестикутник OABCDE. Координати будь-якої його точки задовольняють систему обмежень задачі та умову невід’ємності змінних. Тому поставлену задачу буде розв’язано, якщо ми зможемо відшукати таку точку багатокутника OABCDE, в якій цільова функція Z набирає найбільшого значення.
Для цього побудуємо вектор  , координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор
, координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор  завжди виходить із початку координат і напрямлений до точки з координатами (х1 = с1; х2 = с2). У нашій задачі вектор
завжди виходить із початку координат і напрямлений до точки з координатами (х1 = с1; х2 = с2). У нашій задачі вектор  . Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.
. Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.
Побудуємо лінію, що відповідає, наприклад, значенню Z = 0. Це буде пряма 50х1 + 30х2 = 0, яка перпендикулярна до вектора  і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 50х1 + 30х2 = 0 паралельно самій собі згідно з напрямом вектора
і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 50х1 + 30х2 = 0 паралельно самій собі згідно з напрямом вектора  доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.
доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.
Із рис. 2.14 видно, що останньою спільною точкою прямої цільової функції та багатокутника OABCDE є точка С. Координати цієї точки є оптимальним планом задачі, тобто такими обсягами виробництва книжкових полиць видів А та В, що забезпечують максимум прибутку від їх реалізації за даних умов.
Координати точки С є розв’язком системи рівнянь (2.17) і (2.18):

звідси маємо: х1 = 50; х2 = 60.
Отже, Х* = (50; 60); 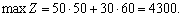
Це означає, що коли фірма щотижня виготовлятиме 50 збірних книжкових полиць моделі А та 60 — моделі В, то вона отримає максимальний прибуток — 4300 у. о. Це потребуватиме повного використання тижневих ресурсів робочого часу верстатів 1 та 2.
 Для невеликої птахоферми потрібно розрахувати оптимальний кормовий раціон на 1000 курчат, яких вирощують з 4-х до 8-тижневого віку. Нехтуючи тим, що потижневі витрати кормів для курчат залежать від їхнього віку, вважатимемо, що за 4 тижні курча споживає не менше 500 г суміші. Крім цього, кормовий раціон курчат має задовольняти певні вимоги щодо поживності. Сформулюємо ці вимоги у спрощеному вигляді, беручи до уваги лише дві поживні речовини: білок і клітковину, що містяться у кормах двох видів — зерні та соєвих бобах. Вміст поживних речовин у кожному кормі та їх вартість маємо у табл. 2.5.
Для невеликої птахоферми потрібно розрахувати оптимальний кормовий раціон на 1000 курчат, яких вирощують з 4-х до 8-тижневого віку. Нехтуючи тим, що потижневі витрати кормів для курчат залежать від їхнього віку, вважатимемо, що за 4 тижні курча споживає не менше 500 г суміші. Крім цього, кормовий раціон курчат має задовольняти певні вимоги щодо поживності. Сформулюємо ці вимоги у спрощеному вигляді, беручи до уваги лише дві поживні речовини: білок і клітковину, що містяться у кормах двох видів — зерні та соєвих бобах. Вміст поживних речовин у кожному кормі та їх вартість маємо у табл. 2.5.
Таблиця 2.5
ПОЖИВНІСТЬ ТА ВАРТІСТЬ КОРМІВ
Корм |
Вміст поживних речовин в 1 кг корму, % |
Вартість 1 кг корму, у. о. |
|
білку |
клітковини |
||
Зерно |
10 |
2 |
0,40 |
Соєві боби |
50 |
8 |
0,90 |
Готова кормова суміш має містити не менше як 20 % білка і не більш як 5 % клітковини.
Визначити масу кожного з двох видів кормів, що утворюють кормову суміш мінімальної вартості, водночас задовольняючи вимоги до загальної маси кормової суміші та її поживності.
Побудова економіко-математичної моделі. Нехай х1 — маса зерна, а х2 — соєвих бобів (в кг) у готовій кормовій суміші.
Загальна кількість суміші х1 + х2 має становити понад 500 кг, тобто
х1 + х2 ≥ 500.
Розглянемо обмеження щодо поживності кормової суміші.
Суміш має містити не менш як 20 % білка:
10х1 + 50х2 ≥ 20 (х1 + х2),
а також не більше як 5 % клітковини:
2х1 + 8х2 ≤ 5 (х1 + х2).
Загалом математична модель задачі оптимізації кормового раціону має такий вигляд:
min Z = 0,40х1 + 0,90х2 (2.26)
за умов:

 (2.30)
(2.30)
Розв’язання. Графічну інтерпретацію задачі подано на рис. 2.15. Множина допустимих її розв’язків необмежена. Для вектора  = (0,4; 0,9) можна змінити масштаб, наприклад,
= (0,4; 0,9) можна змінити масштаб, наприклад,  = (200; 450). Найменшого значення цільова функція Z досягає в точці А, що лежить на перетині граничних прямих, які відповідають обмеженням (2.27) та (2.28). Визначимо її координати:
= (200; 450). Найменшого значення цільова функція Z досягає в точці А, що лежить на перетині граничних прямих, які відповідають обмеженням (2.27) та (2.28). Визначимо її координати:

Отже, Х* = (375; 125); min Z = 0,4 • 375 + 0,9 • 125 = 262,5.
Згідно з відшуканим оптимальним планом задачі для того, щоб отримати 500 кг кормової суміші мінімальної вартості (262,50 у. о.), потрібно взяти 375 кг зерна та 125 кг соєвих бобів. За такого співвідношення компонентів кормової суміші вимоги до її поживності виконуватимуться:
0,10 • 375 + 0,50 • 125 = 100 кг білка, що становить рівно 20 % загальної маси суміші;
0,02 • 375 + 0,08 • 125 = 17,5 кг клітковини в кормовій суміші, що становить 3,5% її маси і не перевищує 5%.

 Фірма виготовляє з одного виду сировини два продукти А та В, що продаються відповідно за 8 та 15 копійок за упаковку. Ринок збуту для кожного з них практично необмежений. Сировина для продукту А обробляється верстатом 1, а для продукту В — верстатом 2. Потім обидва продукти упаковуються на фабриці. Схему виробництва продуктів А та В зображено на рис. 2.16.
Фірма виготовляє з одного виду сировини два продукти А та В, що продаються відповідно за 8 та 15 копійок за упаковку. Ринок збуту для кожного з них практично необмежений. Сировина для продукту А обробляється верстатом 1, а для продукту В — верстатом 2. Потім обидва продукти упаковуються на фабриці. Схему виробництва продуктів А та В зображено на рис. 2.16.

Рис. 2.16. Схема виготовлення продуктів
Ціна 1 кг сировини — 6 копійок. Верстат 1 обробляє за годину 5 т сировини, а верстат 2—4 т сировини із втратами, що становлять відповідно 10 і 20%. Верстат 1 може працювати 6 год на день, причому його використання коштує 288 грн/год; верстат 2—5 год на день, що коштує 336 грн/год.
Маса продукту А в одній упаковці дорівнює 1/4 кг, а продукту В — 1/3 кг. Фабрика може працювати 10 год на день, щогодини упаковуючи 12 000 одиниць продукту А або 8000 одиниць продукту В. Вартість її роботи протягом 1 год становить 360 грн.
Необхідно відшукати такі значення х1 та х2 обсягів використання сировини для виготовлення продуктів А та В (у тоннах), які забезпечують найбільший щоденний прибуток фірми.
Побудова економіко-математичної моделі. Нехай х1 та х2 — відповідно обсяги сировини, використовувані для виготовлення продукту А та В за один день, т.
Запишемо обмеження задачі. Згідно з умовою обмеженими ресурсами є тривалість використання верстатів 1 і 2, а також тривалість роботи фабрики з упакування продуктів А та В.
1. Обмеження на використання верстата 1.
Економічний зміст цього обмеження такий: фактична тривалість використання верстата 1 з обробки сировини для виготовлення продукту А має не перевищувати 6 год, тобто:

Математично це запишеться так:
х1 / 5 ≤6, або х1 ≤ 30.
2. Обмеження щодо використання верстата 2 виразимо аналогічно:
х2 / 4 ≤ 5, або х2 ≤ 20.
3. Обмеження щодо тривалості роботи фабрики з упакування продуктів А та В.
Економічний зміст цього обмеження такий: фактична кількість часу, витраченого на упакування продуктів А та В, має не перевищувати 10 год на день:

Математично це запишеться так:

або:
0,3х1 + 0,3х2 ≤ 10,
3х1 + 3х2 ≤ 100.
Побудуємо цільову функцію задачі. Прибуток фірми дорівнює різниці між доходом від реалізації виготовленої продукції та витратами на її виробництво.
1. Дохід від виробництва продуктів А та В визначається так:

або
 .
.
Загальний дохід дорівнює 288х1 + 360х2.
2. Витрати на сировину визначаємо як загальну кількість сировини в тоннах, використовуваної для виробництва продуктів А та В, помножену на вартість 1 т сировини у гривнях:
60 (х1 + х2) = 60х1 + 60х2 .
3. Витрати, пов’язані з використанням верстатів 1 і 2, визначаємо множенням фактичної тривалості роботи верстата з обробки сировини на вартість 1 год роботи відповідного верстата:
 .
.
4. Витрати, пов’язані з упакуванням продуктів А та В, дорівнюють добутку фактичної тривалості роботи фабрики (0,3х1 + + 0,3х2) на вартість 1 год її роботи, яка становить 360 грн:
360 (0,3х1 + 0,3х2) = 108х1 + 108х2.
Беручи до уваги всі складові цільової функції, можна записати математичний вираз прибутку фірми за день:
Z = (288х1 + 360х2) – (60х1 + 60х2) – (288/5х1 + 84х2) – (108х1 + + 108х2) = 12/5 • (26х1 + 45х2).
Отже, маємо такий остаточний запис економіко-математичної моделі:
max Z = 12/5 • (26х1 + 45х2) (2.31)
за умов:

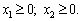 (2.35)
(2.35)
Незважаючи на порівняно складний процес моделювання, математично ця задача дуже проста й легко розв’язується графічно.
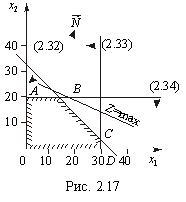 Розв’язання. Графічне розв’язання задачі ілюструє рис. 2.17.
Розв’язання. Графічне розв’язання задачі ілюструє рис. 2.17.
Областю допустимих планів, що утворюється системою обмежень задачі, є багатокутник АВСDО. Найбільшого значення цільова функція досягає у вершині В. Координати цієї точки визначаються розв’язанням системи рівнянь:

Оптимальний план задачі: Х* = (40/3; 20); max Z = 2992 грн.
Отже, для того, щоб отримати найбільший денний прибуток 2992 грн, фірма має обробляти 40/3 тис. кг сировини, виробляючи продукт А, і 20 тис. кг — виробляючи продукт В. За такого оптимального плану випуску продукції верстат 2 працюватиме 20/4 = 5 год на день, тобто з повним навантаженням, а верстат 1 працюватиме лише 40/15 = 2 год 20 хв щодня.
Created/Updated: 25.05.2018
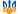 |
|