- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
3.7. Параметричне програмування
У параграфі 3.5 було розглянуто, як змінюється оптимальний план задачі лінійного програмування, якщо змінюються коефіцієнти цільової функції чи компоненти вектора обмежень. Однак дослідження стосувалися лише визначення діапазону змін, у межах якого структура оптимального плану залишалась тією самою, до того ж кожного разу розглядали вплив зміни лише однієї складової.
Однак на практиці трапляються випадки, коли коефіцієнти цільової функції чи компоненти вектора обмежень залежать від якогось одного чинника, наприклад часу, і потрібно знайти розв’язок задачі за будь-якої зміни цього показника, який називають параметром задачі.
Параметричне програмування — це метод визначення залежності змін розв’язку задачі від зміни вектора коефіцієнтів цільової функції чи вектора обмежень.
3.7.1. Параметричні зміни вектора обмежень
Розглянемо задачу лінійного програмування у разі лінійної залежності компонентів вектора обмежень від параметра t. Нехай:
 ,
,  ,
,  . (3.65)
. (3.65)
Тоді задачу лінійного програмування сформулюємо у вигляді:
 (3.66)
(3.66)
 (3.67)
(3.67)
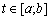
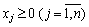 . (3.68)
. (3.68)
Очевидно, що для кожного фіксованого значення 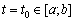 задача (3.66)—(3.68) є звичайною задачею лінійного програмування і може бути розв’язана симплексним методом.
задача (3.66)—(3.68) є звичайною задачею лінійного програмування і може бути розв’язана симплексним методом.
У разі визначення розв’язку задачі, придатного для довільного можливого значення параметра 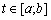 , потрібні розв’язки іноді вдається знаходити за допомогою дещо видозміненого алгоритму симплексного методу.
, потрібні розв’язки іноді вдається знаходити за допомогою дещо видозміненого алгоритму симплексного методу.
Нехай  . Тоді згідно з першою теоремою двоїстості оптимальний план прямої задачі (як і кожен поточний опорний план) можна подати у вигляді:
. Тоді згідно з першою теоремою двоїстості оптимальний план прямої задачі (як і кожен поточний опорний план) можна подати у вигляді:
 , (3.69)
, (3.69)
де D — матриця, що складена з компонент векторів останнього базису; 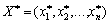 — оптимальний план задачі (3.66)—(3.68); В — вектор, що складається з вільних членів системи обмежень в останній симплексній таблиці.
— оптимальний план задачі (3.66)—(3.68); В — вектор, що складається з вільних членів системи обмежень в останній симплексній таблиці.
Отже, якщо змінюються компоненти вектора В, то змінюються також значення вектора  . У векторній формі (3.65) має вигляд:
. У векторній формі (3.65) має вигляд:
 , (3.70)
, (3.70)
де В — вектор з компонентами bi, а вектор Р складається з компонент рі виразу (3.65). Використовуючи (3.69), маємо:
 . (3.71)
. (3.71)
Добутком  буде вектор, який позначимо через
буде вектор, який позначимо через  , а результатом множення
, а результатом множення  на
на  — вектор
— вектор 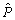 , тоді:
, тоді:
 . (3.72)
. (3.72)
Допустимо, що задачу (3.66)—(3.68) розв’язано, і остання симплексна таблиця має вид:
Таблиця 3.5
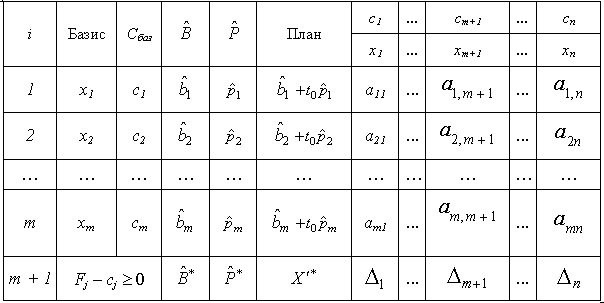
Таблиця містить два додаткових стовпчики, що дає змогу стежити за перетвореннями величин 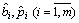 після здійснених ітерацій.
після здійснених ітерацій.
Оскільки таблиця 3.5 містить за допущенням оптимальний план задачі (3.66)—(3.68) 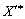 , то має виконуватися умова невід’ємності всіх компонент вектора (3.72), отже,
, то має виконуватися умова невід’ємності всіх компонент вектора (3.72), отже,
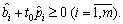 (3.73)
(3.73)
Допустимо тепер, що у формулі (3.73) параметр t0 не фіксований, а може набувати довільних значень на заданому інтервалі [а; b]. Якщо для всіх цих значень параметра нерівності (3.73) задовольняються, тобто
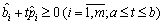 , (3.74)
, (3.74)
то це означає, що знайдений план 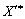 оптимальний для всіх значень
оптимальний для всіх значень 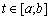 і є розв’язком параметричної задачі (3.66)—(3.68). Проте в загальному випадку нехай за певних значень
і є розв’язком параметричної задачі (3.66)—(3.68). Проте в загальному випадку нехай за певних значень 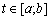 нерівності (3.73) не задовольняються і план
нерівності (3.73) не задовольняються і план  уже не буде оптимальним. Тому необхідно виявити множину всіх значень
уже не буде оптимальним. Тому необхідно виявити множину всіх значень 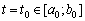 (де проміжок [а0; b0] менший, ніж [а; b]), для яких знайдений план є оптимальним, і, виключивши її з подальшого розгляду, знаходити оптимальний план для другої множини точок з інтервалу
(де проміжок [а0; b0] менший, ніж [а; b]), для яких знайдений план є оптимальним, і, виключивши її з подальшого розгляду, знаходити оптимальний план для другої множини точок з інтервалу  і т. д. Отже, процес розв’язання параметричної задачі передбачає послідовний поділ заданого проміжку
і т. д. Отже, процес розв’язання параметричної задачі передбачає послідовний поділ заданого проміжку  зміни параметра t на ряд таких підпроміжків, щоб для всіх значень
зміни параметра t на ряд таких підпроміжків, щоб для всіх значень  того самого підпроміжку оптимум цільової функції досягався в одній точці (вершині) багатогранника планів задачі, але щоб кожному підпроміжку зміни параметра відповідав окремий оптимальний план.
того самого підпроміжку оптимум цільової функції досягався в одній точці (вершині) багатогранника планів задачі, але щоб кожному підпроміжку зміни параметра відповідав окремий оптимальний план.
Отже, розв’язування параметричної задачі (3.66)—(3.68) починають з деякого значення  і записують задачу (3.66)—(3.68) у вигляді початкової симплексної таблиці, що має вигляд, аналогічний таблиці 3.5. Знаходять симплексним методом оптимальний план задачі (якщо він існує) для даного значення параметра (таблиця 3.5). Зазначимо, що значення компонент оптимального плану подається у вигляді двох доданків, що містяться в двох додаткових стовпчиках
і записують задачу (3.66)—(3.68) у вигляді початкової симплексної таблиці, що має вигляд, аналогічний таблиці 3.5. Знаходять симплексним методом оптимальний план задачі (якщо він існує) для даного значення параметра (таблиця 3.5). Зазначимо, що значення компонент оптимального плану подається у вигляді двох доданків, що містяться в двох додаткових стовпчиках 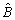 та
та  . Загальні значення цільової функції оптимального плану розраховують додаванням до суми стовпця
. Загальні значення цільової функції оптимального плану розраховують додаванням до суми стовпця  суми стовпця
суми стовпця 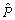 , помноженої на
, помноженої на  (згідно з 3.72). Отже, величина
(згідно з 3.72). Отже, величина  є лінійною функцією параметра t.
є лінійною функцією параметра t.
Визначимо границі значень параметра t,для яких вектор  буде оптимальним планом. Для цього з остаточної таблиці 3.5, де
буде оптимальним планом. Для цього з остаточної таблиці 3.5, де  , складаємо і розв’язуємо систему нерівностей (3.74). У разі існування оптимального плану задачі при
, складаємо і розв’язуємо систему нерівностей (3.74). У разі існування оптимального плану задачі при 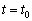 система нерівностей (3.74), очевидно, сумісна, оскільки існує хоча б один її розв’язок. Зрозуміло також, що обов’язково деякі з
система нерівностей (3.74), очевидно, сумісна, оскільки існує хоча б один її розв’язок. Зрозуміло також, що обов’язково деякі з  , бо інакше параметричної задачі не було б. Слід розрізняти два випадки при розв’язанні системи нерівностей (3.74):
, бо інакше параметричної задачі не було б. Слід розрізняти два випадки при розв’язанні системи нерівностей (3.74):
а) Якщо існують такі значення і,для яких 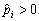 , тоді розв’язками відповідних нерівностей будуть:
, тоді розв’язками відповідних нерівностей будуть:
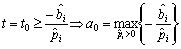 , (3.75)
, (3.75)
що дає нижню границю шуканого інтервалу, яка може дорівнювати а або бути меншою за неї: а0 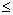 а.
а.
Якщо немає 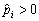 , тобто всі
, тобто всі  , то значення t, для яких знайдений план
, то значення t, для яких знайдений план  буде оптимальним, знизу не обмежені, тобто
буде оптимальним, знизу не обмежені, тобто  .
.
б) Якщо існують такі значення і,для яких 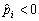 , то розв’язками відповідних нерівностей будуть:
, то розв’язками відповідних нерівностей будуть:
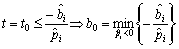 . (3.76)
. (3.76)
В такому разі розв’язок системи нерівностей дає верхню границю шуканого інтервалу, яка може дорівнювати або бути більшою за а (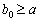 ). Якщо немає
). Якщо немає  , тобто всі
, тобто всі  , то сукупність значень t, для яких знайдений план
, то сукупність значень t, для яких знайдений план  буде оптимальним, зверху необмежена (
буде оптимальним, зверху необмежена ( ), і в цьому останньому разі задача розв’язана повністю, оскільки
), і в цьому останньому разі задача розв’язана повністю, оскільки
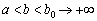 .
.
Отже, для верхньої границі шуканого інтервалу дістаємо формулу:
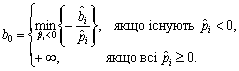 (3.77)
(3.77)
Аналогічна формула для нижньої границі має вигляд:
 (3.78)
(3.78)
За найменшого виходу величини t за межі визначеного інтервалу [a0; b0] значення нового оптимального плану  буде від’ємним (порушуватимуться умови системи нерівностей (3.74)).
буде від’ємним (порушуватимуться умови системи нерівностей (3.74)).
Тобто (3.74) визначає вектор, який необхідно вивести з базису. Припустимо, що за деякого  , де
, де  , мінімальне значення в (3.77), яке визначає верхню границю інтервалу
, мінімальне значення в (3.77), яке визначає верхню границю інтервалу  , досягається для
, досягається для 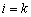 . Отже, порушується k-та нерівність із (3.74), і з базису необхідно виводити вектор, що відповідає змінній
. Отже, порушується k-та нерівність із (3.74), і з базису необхідно виводити вектор, що відповідає змінній 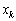 . Тому при
. Тому при 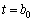 необхідно здійснити зміну базису, для чого виконують один крок двоїстого симплекс-методу, розглянутого в § 3.6., і визначають нове значення
необхідно здійснити зміну базису, для чого виконують один крок двоїстого симплекс-методу, розглянутого в § 3.6., і визначають нове значення  .
.
Далі розглядають знову систему нерівностей (3.74). Для  за формулою (3.77) визначають верхню границю
за формулою (3.77) визначають верхню границю  тих значень t, для яких відшуканий план
тих значень t, для яких відшуканий план  буде оптимальним. Таку процедуру повторюють доти, поки не отримають значення верхньої границі чергового інтервалу, що дорівнює або перевищує верхню границю заданого інтервалу
буде оптимальним. Таку процедуру повторюють доти, поки не отримають значення верхньої границі чергового інтервалу, що дорівнює або перевищує верхню границю заданого інтервалу 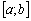 можливих значень t, тобто
можливих значень t, тобто
 . (3.79)
. (3.79)
Співвідношення (3.79) і є ознакою того, що задачу розв’язано.
Отже, заданий проміжок [a; b] поділяють на ряд інтервалів [a; b0], [b1; b2], … [bs–1; b], для кожного з яких максимум цільової функції досягається за відповідного йому одного оптимального плану.
Created/Updated: 25.05.2018
 |
|