- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
8.2. Геометрична інтерпретація задачі нелінійного програмування
Геометрично цільова функція (8.1) визначає деяку поверхню, а обмеження (8.2)—(8.3) — допустиму підмножину n-вимірного евклідового простору. Знаходження оптимального розв’язку задачі нелінійного програмування зводиться до відшукання точки з допустимої підмножини, в якій досягається поверхня найвищого (найнижчого) рівня.
Якщо цільова функція неперервна, а допустима множина розв’язків замкнена, непуста і обмежена, то глобальний максимум (мінімум) задачі існує.
Найпростішими для розв’язування є задачі нелінійного програмування, що містять систему лінійних обмежень та нелінійну цільову функцію. В цьому разі область допустимих розв’язків є опуклою, непустою, замкненою, тобто обмеженою.
Розглянемо приклад геометричного способу розв’язування задачі нелінійного програмування.
 Знайти мінімальне і максимальне значення функції:
Знайти мінімальне і максимальне значення функції:
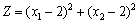
за умов:
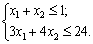
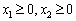 .
.
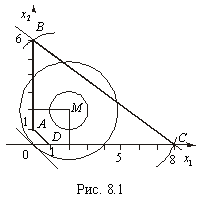 Розв’язання. Область допустимих розв’язків утворює чотирикутник АВСD (рис. 8.1). Геометрично цільова функція являє собою коло з центром у точці М (2; 2), квадрат радіуса якого
Розв’язання. Область допустимих розв’язків утворює чотирикутник АВСD (рис. 8.1). Геометрично цільова функція являє собою коло з центром у точці М (2; 2), квадрат радіуса якого 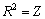 . Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція Z має два локальних максимуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках:
. Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція Z має два локальних максимуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках:
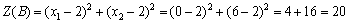 ,
,
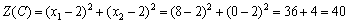 .
.
Оскільки 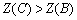 , то точка С (8; 0) є точкою глобального максимуму.
, то точка С (8; 0) є точкою глобального максимуму.
Очевидно, що найменший радіус 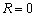 , тоді:
, тоді:
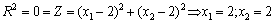 . Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
. Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
Зазначимо, що в даному разі точка, яка відповідає оптимальному плану задачі (мінімальному значенню функціонала), знаходиться всередині багатокутника допустимих розв’язків, що в задачах лінійного програмування неможливо.
 Знайти мінімальне значення функції:
Знайти мінімальне значення функції:
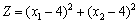
за умов:
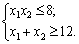
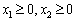 .
.
Розв’язування. У даному прикладі множина допустимих розв’язків складається з двох окремих частин, необмежених зверху (рис. 8.2). Цільова функція аналогічно попередньому випадку є колом з центром у точці М (4; 4). Функція Z має два локальних мінімуми: в точці А (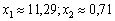 ), і в точці В (
), і в точці В (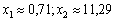 ).
).
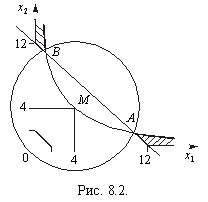 Значення функціонала в цих точках однакове і дорівнює:
Значення функціонала в цих точках однакове і дорівнює:
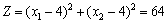 .
.
Отже, маємо два альтернативні оптимальні плани.
Даний приклад ілюструє ще одну особливість задач нелінійного програмування: на відміну від задач лінійного програмування багатогранник допустимих розв’язків задачі нелінійного програмування не обов’язково буде опуклою множиною.
Наведемо основні особливості задач нелінійного програмування, що зумовлюють необхідність застосування відповідних методів їх розв’язання.
Created/Updated: 25.05.2018
 |
|