- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
8.6.1. Опуклі й угнуті функції
Наведемо основні означення та теореми. Нехай задано n-вимірний лінійний простір Rn. Функція  , що задана на опуклій множині
, що задана на опуклій множині  , називається опуклою, якщо для будь-яких двох точок
, називається опуклою, якщо для будь-яких двох точок  та
та  з множини X і будь-яких значень
з множини X і будь-яких значень  виконується співвідношення:
виконується співвідношення:
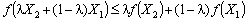 . (8.27)
. (8.27)
Якщо нерівність строга і виконується для  , то функція
, то функція 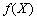 називається строго опуклою.
називається строго опуклою.
Функція  , яка задана на опуклій множині
, яка задана на опуклій множині  , називається угнутою, якщо для будь-яких двох точок
, називається угнутою, якщо для будь-яких двох точок 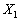 та
та  з множини X і будь-якого
з множини X і будь-якого  справджується співвідношення:
справджується співвідношення:
 . (8.28)
. (8.28)
Якщо нерівність строга і виконується для  , то функція
, то функція  називається строго угнутою.
називається строго угнутою.
Слід зазначити, що опуклість та угнутість функції визначаються лише відносно опуклих множин у  , оскільки за наведеними означеннями разом з двома будь-якими точками
, оскільки за наведеними означеннями разом з двома будь-якими точками  та
та  множині X належать також точки їх лінійної комбінації:
множині X належать також точки їх лінійної комбінації:  для всіх значень
для всіх значень  , що можливо лише у разі, коли множина X є опуклою.
, що можливо лише у разі, коли множина X є опуклою.
Теорема 8.2. Нехай  — опукла функція, що задана на замкненій опуклій множині X, тоді будь-який локальний мінімум
— опукла функція, що задана на замкненій опуклій множині X, тоді будь-який локальний мінімум  на цій множині є і глобальним.
на цій множині є і глобальним.
Доведення. Допустимо, що в точці 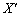 функція
функція  має локальний мінімум, тоді як глобальний мінімум досягається в точці
має локальний мінімум, тоді як глобальний мінімум досягається в точці  , отже, виконуватиметься нерівність
, отже, виконуватиметься нерівність  . Через те що
. Через те що  — опукла функція, для будь-яких значень
— опукла функція, для будь-яких значень  справджується співвідношення:
справджується співвідношення:
 . (8.29)
. (8.29)
Множина Х опукла, тому точка  при
при  також належить цій множині. Враховуючи, що
також належить цій множині. Враховуючи, що  , нерівність (8.29) матиме вигляд:
, нерівність (8.29) матиме вигляд:
 ;
;
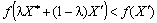 .
.
Значення 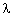 можна вибрати так, щоб точка
можна вибрати так, щоб точка  була розташована як завгодно близько до
була розташована як завгодно близько до  . Тоді отримана остання нерівність суперечить тому, що
. Тоді отримана остання нерівність суперечить тому, що  — точка локального мінімуму, оскільки існує як завгодно близька до неї точка, в якій функція набуває меншого значення, ніж у точці
— точка локального мінімуму, оскільки існує як завгодно близька до неї точка, в якій функція набуває меншого значення, ніж у точці  . Тому попереднє допущення неправильне. Теорему доведено.
. Тому попереднє допущення неправильне. Теорему доведено.
Теорема 8.3. Нехай  — опукла функція, що визначена на опуклій множині Х, і крім того, вона неперервна разом з частинними похідними першого порядку в усіх внутрішніх точках Х. Нехай
— опукла функція, що визначена на опуклій множині Х, і крім того, вона неперервна разом з частинними похідними першого порядку в усіх внутрішніх точках Х. Нехай  — точка, в якій
— точка, в якій  . Тоді в точці
. Тоді в точці  досягається локальний мінімум, що збігається з глобальним.
досягається локальний мінімум, що збігається з глобальним.
Доведення. З рівності (8.12) для  знаходимо:
знаходимо:
 ;
;

 ;
;

 .
.
Через те що існують частинні похідні першого порядку, функцію  можна розкласти в ряд Тейлора:
можна розкласти в ряд Тейлора:
 ,
,
де 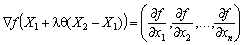 — градієнт функції f, обчислений у точці
— градієнт функції f, обчислений у точці 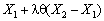 ,
,  . Тоді:
. Тоді:


 .
.
Переходимо до границі при  , отримаємо:
, отримаємо:

 . (8.30)
. (8.30)
Ця умова виконується для будь-яких внутрішніх точок Х1 та Х2 і є необхідною і достатньою умовою опуклості f(X).
Якщо функція f(X) неперервна разом з частинними похідними першого порядку і угнута на множині Х, то аналогічно попередньому результату маємо:

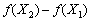 .
.
Припустимо, що Х0 — довільна точка множини Х, тоді, взявши  ,
, 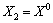 , а також за умовою теореми
, а також за умовою теореми  , в нерівності (8.30) маємо:
, в нерівності (8.30) маємо:

 .
.
Отже, опукла функція f(X) досягає свого глобального мінімуму на множині Х у кожній точці, де 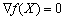 . Теорему доведено.
. Теорему доведено.
Як наслідок теореми можна показати, що коли Х замкнена, обмежена знизу, опукла множина, то глобального максимуму опукла функція f(X) досягає на ній у одній чи кількох точках (при цьому допускається, що в точці Х значення функції скінченне). Застосовуючи за розв’язування таких задач процедуру перебору крайніх точок, можна отримати точку локального максимуму, однак не можна встановити, чи є вона точкою глобального максимуму.
Для угнутих функцій отримані результати формулюють так. Нехай f(X) — угнута функція, що задана на замкненій опуклій множині 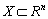 . Тоді будь-який локальний максимум f(X) на множині Х є глобальним. Якщо глобальний максимум досягається в двох різних точках множини, то він досягається і на нескінченній множині точок, що лежать на відрізку, який сполучає ці точки. Для строго угнутої функції існує єдина точка, в якій вона досягає глобального максимуму.
. Тоді будь-який локальний максимум f(X) на множині Х є глобальним. Якщо глобальний максимум досягається в двох різних точках множини, то він досягається і на нескінченній множині точок, що лежать на відрізку, який сполучає ці точки. Для строго угнутої функції існує єдина точка, в якій вона досягає глобального максимуму.
Градієнт угнутої функції f(X) у точках максимуму дорівнює нулю, якщо f(X) — диференційовна функція. Глобальний мінімум угнутої функції, якщо він скінченний на замкненій обмеженій зверху множині, має досягатися в одній чи кількох її крайніх точках за умови скінченності функції f(X) у кожній точці цієї множини.
Created/Updated: 25.05.2018
 |
|