- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
9.2. Задача про розподіл капіталовкладень між двома підприємствами на n років
Розглянемо задачу динамічного програмування на прикладі задачі про розподіл капіталовкладень.
Допустимо, що розглядається виробнича система, яка складається з двох підприємств. Нехай плановий період складається з n інтервалів-частин (наприклад, років), і протягом даного періоду слід використати суму коштів b, що має бути розподілена між двома підприємствами. Відомі прибутки, які приносять вкладення коштів: вкладення у перше підприємство обсягом x приносить прибуток 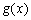 , а друге підприємство дає з такої ж суми прибутку
, а друге підприємство дає з такої ж суми прибутку 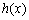 .
.
Необхідно розподілити кошти на період у n років так, щоб досягти максимального прибутку за весь плановий період.
Можна легко сформулювати задачу, коли плановий період складається з одного року (однокрокова задача).
Якщо в перше підприємство здійснили вкладення обсягом x, тоді сума вкладених у друге підприємство коштів становить 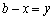 і дає прибуток
і дає прибуток 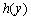 .
.
У такому разі маємо однокрокову задачу:
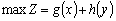
за умов:
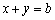 ,
,
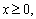
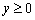 .
.
Введемо позначення:
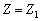 ,
, 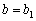 ,
, 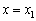 ,
, 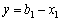 , тоді задача матиме вигляд:
, тоді задача матиме вигляд:
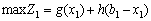 ; (9.1)
; (9.1)
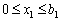 . (9.2)
. (9.2)
Тепер розглянемо цю задачу оптимального розподілу капітальних вкладень, якщо вона складається з двох періодів (етапів).
Оскільки прибуток утворюється в результаті випуску та реалізації продукції, що пов’язано з певними виробничими витратами, то на початок другого періоду початкова сума 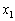 зменшиться до величини
зменшиться до величини 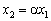 , де
, де 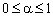 , а сума
, а сума 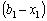 — до величини
— до величини 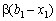 , де
, де 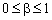 . Щоб визначити найбільший прибуток, який можна отримати від сумарного залишку
. Щоб визначити найбільший прибуток, який можна отримати від сумарного залишку 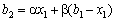 протягом другого етапу, необхідно розв’язати задачу математичного програмування, аналогічну до задачі (9.1)—(9.2), тобто:
протягом другого етапу, необхідно розв’язати задачу математичного програмування, аналогічну до задачі (9.1)—(9.2), тобто:
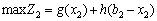 , (9.3)
, (9.3)
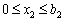 . (9.4)
. (9.4)
Поставимо тепер задачу оптимального поточного планування розподілу капіталовкладень по всіх n інтервалах періоду, причому принцип розподілу вкладень у кожному з періодів полягає у відшуканні оптимального використання тієї суми коштів, що залишається на кінець попереднього періоду. Критерій оптимальності не змінюється і полягає в максимізації прибутку за весь період. Тоді для k-го етапу (періоду) залишок коштів після використання в попередньому періоді становитиме 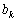 . Визначаємо оптимальну суму коштів
. Визначаємо оптимальну суму коштів 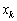 , що доцільно вкладати в перше підприємство в k-му періоді, розв’язуючи таку задачу:
, що доцільно вкладати в перше підприємство в k-му періоді, розв’язуючи таку задачу:
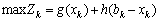 , (9.5)
, (9.5)
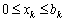 . (9.6)
. (9.6)
Оскільки критерієм оптимальності є максимізація загального прибутку за всі n періодів, то в цілому необхідно знайти максимальне значення функціонала, що складається із максимальних значень прибутків кожного окремого періоду, тобто загальна задача має вид:
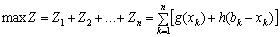 (9.7)
(9.7)
за умов:
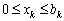
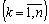 , (9.8)
, (9.8)
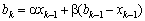
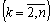 .
.
Цільова функція (9.7) є функцією n змінних 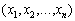 і залежить від початкового параметра
і залежить від початкового параметра 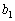 .
.
Розв’язування задачі (9.7)—(9.8) розглянутими раніше однокроковими методами може виявитися неможливим. Проте міркування, які привели до формулювання задачі (9.7)—(9.8), породжують ідею побудови алгоритму поетапного розв’язування динамічних задач.
Created/Updated: 25.05.2018
 |
|