- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
10.2. Особливості математичної постановки задач стохастичного програмування
В задачах детермінованого характеру за певним набором початкових даних однозначно визначається вигляд цільової функції та обмежень задачі. У стохастичному програмуванні особливості побудови математичних моделей задач пов’язані з можливостями вибору виду функції мети та обмежень, тобто за одного набору початкових значень можна отримати математичні моделі, що суттєво відрізнятимуться, а отже, значні розбіжності матимуть і отримані за ними оптимальні плани. Розглянемо основні відмінності будови математичних моделей задач стохастичного програмування.
Довільна математична модель задачі математичного програмування складається з двох частин: цільової функції і обмежень. У задачах стохастичного програмування важливим є вибір як виду цільової функції так і виду обмежень. Цільова функція визначає ефективність функціонування і розвитку економічної системи. Якщо відомі основні характеристики випадкових параметрів задачі, то цільовою функцією може бути:
- максимізація математичного сподівання відповідного економічного показника (прибутку, рівня рентабельності тощо); в такому разі задачі мають назву М-моделей;
- мінімізація дисперсії деякого економічного показника за умови обмеження на певному бажаному рівні середньої величини того ж показника, тоді задачі мають назву V-моделей;
- ймовірність перевищення (неперевищення) економічним показником певного фіксованого рівня (порога), тоді задача належить до Р-моделей.
Обмеження в стохастичних економіко-математичних моделях можуть також задаватися різними способами, а значить, отримані оптимальні плани будуть мати відповідний рівень ймовірності їх виконання. При цьому потрібно брати до уваги як внутрішню невизначеність (технологічних процесів), так і невизначеність зовнішнього середовища (постачання сировини, попиту на вироблену продукцію, загальної суми податків тощо).
Нехай задано обмеження задачі математичного програмування в загальному вигляді:
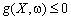 . (10.1)
. (10.1)
Неможливість, а іноді й недоцільність вимоги, щоб знайдене рішення задовольняло обмеження (10.1) за будь-яких реалізацій випадкових параметрів 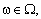 породжує таку ідею: накласти дещо менш жорсткі умови, зокрема замість (10.1) можна допускати невиконання умов з певною ймовірністю. Наприклад:
породжує таку ідею: накласти дещо менш жорсткі умови, зокрема замість (10.1) можна допускати невиконання умов з певною ймовірністю. Наприклад:
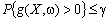 , (10.2)
, (10.2)
або
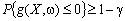 . (10.3)
. (10.3)
Обмеження (10.2) трактується так: ймовірність того, що 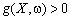 , не перевищує величину γ. Відповідно вираз (10.3) гарантує, що з ймовірністю
, не перевищує величину γ. Відповідно вираз (10.3) гарантує, що з ймовірністю 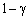 буде виконуватися обмеження (10.1). Наприклад, якщо
буде виконуватися обмеження (10.1). Наприклад, якщо 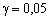 , то обмеження у 95 випадках із 100 буде виконуватися і тільки у п’яти випадках не буде виконуватися.
, то обмеження у 95 випадках із 100 буде виконуватися і тільки у п’яти випадках не буде виконуватися.
Крім того, система обмежень задачі може бути змішаною, тобто частина обмежень може виконуватися в середньому, частина — в жорсткій постановці, а частина — з деякою ймовірністю.
Наведемо кілька варіантів постановок задач стохастичного програмування.
Нехай 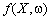 — функція, яка виражає ефективність плану для заданих Х та ω. Тоді задачу визначення оптимального детермінованого плану Х за випадкових параметрів ω можна сформулювати у таких варіантах:
— функція, яка виражає ефективність плану для заданих Х та ω. Тоді задачу визначення оптимального детермінованого плану Х за випадкових параметрів ω можна сформулювати у таких варіантах:
а) 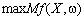 , (10.4)
, (10.4)
за умов:
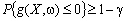 ; (10.5)
; (10.5)
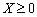 ,
, 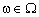 ; (10.6)
; (10.6)
б) 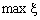 (10.7)
(10.7)
за умов:
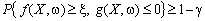 ; (10.8)
; (10.8)
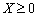 ,
, 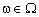 . (10.9)
. (10.9)
Отже, за постановки задачі варіанту а) необхідно максимізувати середню сподівану ефективність за умов, що обмеження, наприклад, щодо ресурсів, виконання контрактів тощо виконуються з імовірністю 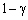 . За постановки задачі варіанту б) крім цього вимагається, щоб значення функції ефективності, наприклад, прибутку було не менше величини ξ з імовірністю
. За постановки задачі варіанту б) крім цього вимагається, щоб значення функції ефективності, наприклад, прибутку було не менше величини ξ з імовірністю 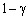 , а також, щоб величина ξ була максимальною. Зазначимо, що перевага варіанту а) полягає у тому, що він простіший стосовно обчислення.
, а також, щоб величина ξ була максимальною. Зазначимо, що перевага варіанту а) полягає у тому, що він простіший стосовно обчислення.
Оскільки у моделі (10.4)—(10.6) як критерій оптимальності використано математичне сподівання 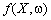 , то маємо М-модель, а плани, отримані за такою моделлю, називають М-планами.
, то маємо М-модель, а плани, отримані за такою моделлю, називають М-планами.
Зрозуміло, що можна формулювати задачі стохастичного програмування також і по-іншому, поєднуючи або комбінуючи у певний спосіб умови наведених вище першої та другої моделей. Так, приміром, задача стохастичного програмування може мати такий вигляд:
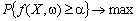 ,
,
за умов:
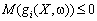
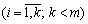 ;
;
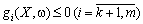 ;
;
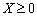
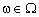 .
.
Отже, очевидно, що конкретних постановок задач стохастичного програмування досить багато і вибір певного їх виду для розв’язування практичних задач залежить від конкретних умов задачі, наявної інформації та мети дослідження.
Постановка задачі стохастичного програмування істотно залежить також від того, чи є можливість під час вибору (прийняття) рішень уточнювати стан економічного середовища (природи) на підставі певних спостережень.
Відомо, що для економічних систем розробляють стратегічні та тактичні плани. Розробляючи стратегічні плани, враховують всі можливі значення ω, тобто стан зовнішнього та внутрішнього середовища, та приймають рішення щодо траєкторії розвитку системи. Однак зустрічаються задачі, коли є можливість провести спостереження над ω (у певний момент стан економічного середовища стає відомим) і вибрати розв’язок з урахуванням результатів спостережень. Наприклад, плануючи виробничу діяльність підприємства, рішення щодо обсягів випуску продукції приймаються з урахуванням дослідження поточного стану структури ринку. Тоді розробляють тактичний план, тобто знаходять рішення 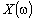 при заданому
при заданому 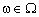 , тобто розв’язують задачу:
, тобто розв’язують задачу:
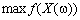 ,
,
за умов:
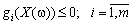 ,
,
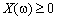 .
.
У загальному випадку спостереження уможливлюють неповне описування стану середовища, а тому етапи вибору рішень можуть чергуватися з етапами спостережень за станом зовнішнього середовища. Отже, відбуваються багатоетапні процеси вибору рішень у такій послідовності:
рішення — спостереження — рішення — спостереження...
або
спостереження — рішення — спостереження — рішення...
Якщо ряд розв’язків починається зі слова «рішення» і воно зустрічається N раз, то модель називають N-етапною задачею (моделлю) стратегічного стохастичного програмування, а якщо зі слова «спостереження» — то задачею (моделлю) тактичного стохастичного програмування.
Кожен з N етапів у свою чергу також може бути поділений. У такому разі маємо одноетапні чи двохетапні задачі стохастичного програмування.
Одноетапна задача стохастичного програмування використовується в тому разі, коли рішення приймаються на підставі відомих характеристик розподілу ймовірностей випадкових параметрів умови задачі до спостережень за їхніми реалізаціями. У такому разі має прийматися найкраще в середньостатистичному розумінні рішення. Тобто випадкові параметри задачі замінюють їх середніми величинами і початкову задачу стохастичного програмування зводять до детермінованої.
Двохетапна задача стохастичного програмування виникає тоді, коли процес прийняття рішення поділяють на два етапи.
 На першому етапі вибирається попередній план, який задовольняє умови задачі за будь-якої реалізації випадкових параметрів. На другому етапі розраховується величина компенсації відхилень розробленого плану від фактичних значень, що були визначені після спостереження за реалізацією випадкових параметрів. Оптимальний план задачі визначають так, щоб забезпечити мінімум середнього значення загальних витрат, які виникають на обох етапах розв’язування задачі. Для існування розв’язку двохетапної задачі вибір плану на першому етапі має гарантувати існування плану-компенсації.
На першому етапі вибирається попередній план, який задовольняє умови задачі за будь-якої реалізації випадкових параметрів. На другому етапі розраховується величина компенсації відхилень розробленого плану від фактичних значень, що були визначені після спостереження за реалізацією випадкових параметрів. Оптимальний план задачі визначають так, щоб забезпечити мінімум середнього значення загальних витрат, які виникають на обох етапах розв’язування задачі. Для існування розв’язку двохетапної задачі вибір плану на першому етапі має гарантувати існування плану-компенсації.
Побудуємо математичну модель відомої задачі про визначення оптимального виробничого плану в термінах стохастичного програмування. Необхідно розрахувати оптимальний план виробництва трьох видів продукції 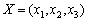 , за якого максимізується загальний прибуток підприємства. Для спрощення розглянемо використання лише двох видів ресурсів, обсяги яких відомі:
, за якого максимізується загальний прибуток підприємства. Для спрощення розглянемо використання лише двох видів ресурсів, обсяги яких відомі: 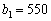 од.,
од., 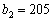 од. Прибуток від реалізації одиниці j-го виду продукції
од. Прибуток від реалізації одиниці j-го виду продукції 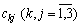 є випадковим, але відомі ймовірності одержання k-ої величини прибутку від реалізації одиниці j-го виду продукції
є випадковим, але відомі ймовірності одержання k-ої величини прибутку від реалізації одиниці j-го виду продукції 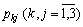 . Норми витрат і-го виду ресурсу на одиницю j-го виду продукції
. Норми витрат і-го виду ресурсу на одиницю j-го виду продукції 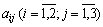 детерміновані. Початкові дані наведені в таблицях 1—4.
детерміновані. Початкові дані наведені в таблицях 1—4.
Таблиця 10.1
Прибуток від одиниці першого виду продукції, ум. од. |
Ймовірність |
10 |
0,3 |
13 |
0,4 |
15 |
0,3 |
Таблиця 10.2
Прибуток від одиниці другого виду продукції, ум. од. |
Ймовірність |
12 |
0,2 |
15 |
0,5 |
13 |
0,3 |
Таблиця 10.3
Прибуток від одиниці третього виду продукції, ум. од. |
Ймовірність |
12 |
0,3 |
11 |
0,5 |
14 |
0,2 |
Таблиця 10.4
Вид продукції |
Норма витрат ресурсів на виготовлення одиниці продукції, ум. од. |
|
першого виду |
другого виду |
|
Перший |
5 |
1 |
Другий |
4 |
2 |
Третій |
3 |
1,5 |
Розв’язання.
Як зазначалось, математична постановка задачі стохастичного програмування може бути подана в різних варіантах залежно від вигляду цільової функції. Розглянемо кілька можливих варіантів постановок для умов даної задачі.
І варіант.
Цільова функція залежить від випадкової величини, отже, математична модель даної задачі має вигляд:
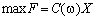 ,
,
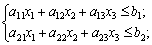
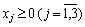 .
.
Маємо одноетапну задачу стохастичного програмування з випадковими параметрами цільової функції. Очевидно, що величина F є також випадковою величиною з законом розподілу ймовірностей 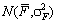 , де
, де 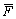 — математичне сподівання, а
— математичне сподівання, а 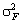 — дисперсія.
— дисперсія.
Щоб розв’язати таку задачу, необхідно знайти математичне сподівання 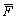 .
.
Позначимо символами 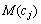 ,
, 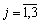 — математичне сподівання прибутку від j-го виду продукції, тоді математична модель набуває вигляду:
— математичне сподівання прибутку від j-го виду продукції, тоді математична модель набуває вигляду:
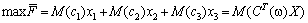 ,
,
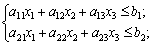
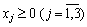 .
.
У наведеній постановці маємо одноетапну задачу стохастичного програмування з М-моделлю, оскільки цільова функція є математичним сподіванням випадкової величини (прибутку).
Оскільки випадкова величина прибутку є дискретною і відомі значення відповідних ймовірностей 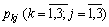 , то можна безпосередньо обчислити значення
, то можна безпосередньо обчислити значення 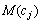
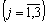 . Отже, в числовому вигляді маємо:
. Отже, в числовому вигляді маємо:
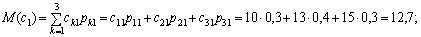
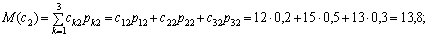
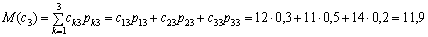 .
.
Математична модель задачі набуває такого вигляду:
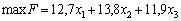 ,
,
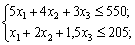
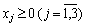 .
.
Початкова задача зведена до задачі лінійного програмування, яку можна розв’язати симплексним методом, але оптимальний план детермінованої задачі є наближеним розв’язком початкової стохастичної.
Оптимальним планом є 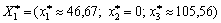 , причому прибуток становить
, причому прибуток становить 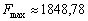 .
.
ІІ варіант.
Отриманий розв’язок може бути основою плану виробництва продукції за даних умов. Однак очевидно, що, оскільки значення випадкових величин були замінені їх математичним сподіванням, то розв’язок задачі знайдено як деяке усереднення всіх можливих за даних умов розв’язків. Для деякого набору фіксованих умов розрахований план може виявитись неоптимальним, тобто справжнє значення прибутку буде значно відрізнятися від очікуваного рівня. Якщо, наприклад, зовнішні умови складаються найнесприятливіше (мінімальні рівні прибутків для кожного з видів продукції), то значення цільової функції для відшуканого оптимального плану буде дорівнювати:
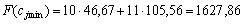 .
.
Очевидно, що відхилення даного значення від середнього очікуваного рівня (1848,78 – 1627,86 = 220,92) показує можливе завищення прибутку у плані. Відомо, що однією з головних характеристик відхилення значень випадкової величини від її середнього є дисперсія. Розрахуємо значення дисперсії для отриманого оптимального плану:
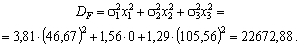
Середнє квадратичне відхилення дорівнює 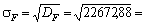
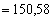 .
.
Якщо допустити, що випадкова величина має нормальний закон розподілу, то, враховуючи властивості середнього квадратичного відхилення (правило трьох «сігм»), визначимо межі, в яких змінюватиметься прибуток: 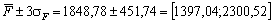 . Якщо розраховані зміни прибутку не можуть влаштовувати особу, що приймає рішення, то доцільно ввести обмеження, яке зменшить ризик втрати доходу.
. Якщо розраховані зміни прибутку не можуть влаштовувати особу, що приймає рішення, то доцільно ввести обмеження, яке зменшить ризик втрати доходу.
За необхідності зменшення можливих втрат прибутку в систему обмежень вводять умову, що дисперсія прибутку має не перевищувати деякої заданої величини. Розв’яжемо задачу з додатковою умовою, що дисперсія має не перевищувати 5000.
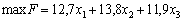 ,
,
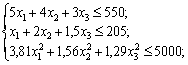
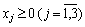 .
.
Ця задача є нелінійною. Розв’язавши її, маємо такий оптимальний план:
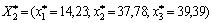 , причому прибуток
, причому прибуток 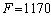 буде змінюватися приблизно на 210 ум. од. (оскільки
буде змінюватися приблизно на 210 ум. од. (оскільки 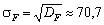 ).
).
ІІІ варіант.
Застосування інструментарію математичного програмування до розв’язання економічних задач уможливлює врахування найвибагливіших побажань стосовно набору властивостей розроблюваних планів. Допустимо, що необхідно, орієнтуючись на деякий середній рівень прибутку, досягти мінімального рівня можливих його змін. У такому разі доречно використати V-модель задачі стохастичного програмування:
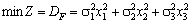 ,
,
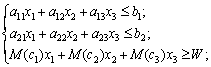
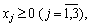
де W — бажаний рівень сподіваного прибутку.
Зафіксуємо бажаний прибуток на рівні не нижче, ніж 1500 ум. од., і знайдемо оптимальний план такої задачі:
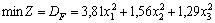 ,
,
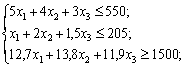
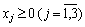 .
.
Розв’язавши цю задачу квадратичного програмування, маємо:
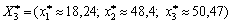 , мінімальна дисперсія сподіваного прибутку буде дорівнювати
, мінімальна дисперсія сподіваного прибутку буде дорівнювати 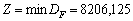 , тобто зміни прибутку відбуватимуться в межах
, тобто зміни прибутку відбуватимуться в межах 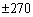 ум. од.
ум. од.
Вибір одного з наведених варіантів математичних моделей залежатиме від конкретної ситуації, поставлених цілей та вимог, однак наведений приклад показує, що використання стохастичних задач дає математично обґрунтовану інформацію, яка може бути основою прийняття рішень за складних реальних умов.
Created/Updated: 25.05.2018
 |
|