- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
8.6. Теорема Куна—Таккера
Розглянутий метод множників Лагранжа уможливлює знаходження лише локальних сідлових точок функції Лагранжа.
Теорема Куна—Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки.
Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:
 , (8.22)
, (8.22)
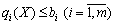 , (8.23)
, (8.23)
 . (8.24)
. (8.24)
(Очевидно, що знак нерівності можна змінити на протилежний множенням лівої і правої частин обмеження на (– 1)).
Теорема 8.1. (Теорема Куна—Таккера). Вектор Х* є оптимальним розв’язком задачі (8.22)—(8.24) тоді і тільки тоді, коли існує такий вектор  , що при
, що при 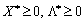 для всіх
для всіх  точка
точка  є сідловою точкою функції Лагранжа
є сідловою точкою функції Лагранжа
 ,
,
і функція мети 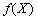 для всіх
для всіх 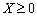 угнута, а функції
угнута, а функції 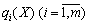 — опуклі.
— опуклі.
Доведення. Необхідність. Нехай Х* — оптимальний план задачі (8.22)—(8.24), тобто є точкою глобального максимуму задачі. Отже, для всіх інших планів задачі Х з множини допустимих розв’язків виконуватиметься співвідношення:
 .
.
Розглянемо тепер вектор  , що відповідає точці глобального максимуму
, що відповідає точці глобального максимуму 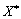 , і значення функції Лагранжа в точках
, і значення функції Лагранжа в точках 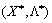 ,
,  ,
,  , де
, де 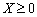 — довільний план задачі з множини допустимих розв’язків,
— довільний план задачі з множини допустимих розв’язків,  — вектор множників Лагранжа, що відповідає Х.
— вектор множників Лагранжа, що відповідає Х.
З умови (8.21) маємо: 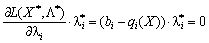 , тоді
, тоді
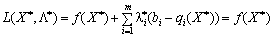 . (8.25)
. (8.25)
Для точки з координатами  деякі доданки виду
деякі доданки виду  можуть бути відмінними від нуля. Оскільки за умовою задачі
можуть бути відмінними від нуля. Оскільки за умовою задачі  , то лише за умови, що
, то лише за умови, що  , матимемо нерівність:
, матимемо нерівність:
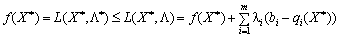 .
.
Функція 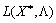 — лінійна відносно
— лінійна відносно  , тобто остання нерівність виконується для будь-якого
, тобто остання нерівність виконується для будь-якого 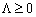 . Отже, точка
. Отже, точка  — точка глобального мінімуму по
— точка глобального мінімуму по  функції Лагранжа.
функції Лагранжа.
Для встановлення нерівності, що відповідає лівій частині умови (8.13), а саме:  , скористаємося також рівнянням (8.21), підсумувавши його по і:
, скористаємося також рівнянням (8.21), підсумувавши його по і:  . За умовою теореми
. За умовою теореми 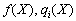 — угнуті функції і
— угнуті функції і 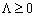 , тому виконується таке рівняння:
, тому виконується таке рівняння:

Отже, у точці Х* функція Лагранжа має глобальний максимум по Х, що повністю доводить необхідність теореми.
Достатність. Для доведення достатності умов теореми потрібно виходити з того, що 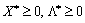 ,
,  — сідлова точка функції
— сідлова точка функції 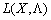 (тобто для
(тобто для 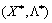 виконується нерівність (8.13)), і необхідно довести, що тоді Х* є оптимальним планом задачі опуклого програмування.
виконується нерівність (8.13)), і необхідно довести, що тоді Х* є оптимальним планом задачі опуклого програмування.
Підставимо у нерівність (8.13) вираз функції Лагранжа (8.12) для задачі (8.22)—(8.23):
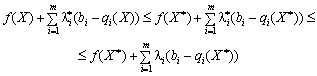 (8.26)
(8.26)
при всіх значеннях  .
.
Розглянемо праву частину подвійної нерівності (8.26).


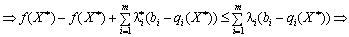
 .
.
Остання нерівність має виконуватися для всіх  . Крім того,
. Крім того, 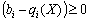 , тобто нерівність справджується лише у разі, коли
, тобто нерівність справджується лише у разі, коли
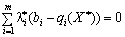 .
.
Тоді з лівої частини нерівності (8.26) маємо:

 .
.
Через те що  , приходимо до нерівності
, приходимо до нерівності 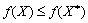 , яка справджується для всіх значень
, яка справджується для всіх значень 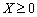 .
.
Отже, точка Х* задовольняє обмеження і надає максимального значення цільовій функції задачі, тому що для всіх інших  функція
функція  набуває менших значень, ніж у точці Х*, тобто вона є оптимальним планом задачі нелінійного програмування. Достатність умов тереми доведено.
набуває менших значень, ніж у точці Х*, тобто вона є оптимальним планом задачі нелінійного програмування. Достатність умов тереми доведено.
Умови теореми Куна — Таккера виконуються лише для задач, що містять опуклі функції.
Created/Updated: 25.05.2018
 |
|